(extrait de Michel Volle, e-conomie, Economica 2000)

L'économie des réseaux est " à coût fixe ", mais pas au même point ni au même sens que celle de l'informatique : c'est une économie du dimensionnement. Les réseaux sont en effet soit des infrastructures dont le coût d'exploitation est quasi nul (routes), soit des automates dont le coût d'exploitation est faible (télécommunications), soit des plates-formes de services dont le coût d'exploitation est élevé mais dépend peu du volume du service produit (transport aérien), soit une juxtaposition de moyens de production au coût de plus en plus élevé mis en œuvre progressivement lorsque la charge du réseau augmente (énergie).

La fonction de production du réseau est à coût fixe, une fois celui-ci construit, car il peut fournir des services dont le coût est nul ou négligeable (communication téléphonique en dehors de l'heure de pointe, sièges libres d'un avion etc.). Cependant, sa construction n'est pas à coût fixe ; le coût du réseau dépend de la dimension que lui donnent ses promoteurs, et sera souvent fonction linéaire de cette dimension : nombre de lignes principales du réseau téléphonique, nombre d'avions d’un transporteur aérien, etc.

1. Période de pointe

À moyen terme l'exploitant du réseau paie un dimensionnement. Le coût de celui-ci, pour une règle d'ingénierie r donnée, est fonction du trafic anticipé en période de pointe t^a :

c = f( r; t^a).

Le trafic en dehors de la période de pointe a un coût de moyen terme nul (puisqu'il ne conduit pas à réviser l'anticipation t^a) et un coût de court terme soit nul (trafic télécoms en dehors de l'heure de pointe), soit très faible (passager qui occupe un siège d'avion qui autrement serait resté libre).

Le trafic qui excède la capacité en heure de pointe est refoulé : il a donc un coût de court terme nul, mais son coût de moyen terme ne l'est pas car sa prise en compte induit une révision de l'anticipation t^a.

La définition de l'heure de pointe, ainsi que du taux de blocage du trafic jugé admissible à l'heure de pointe, est un enjeu important du dimensionnement. Les opérateurs télécoms définissent deux périodes de pointe : l'une s'étale sur les heures de bureau du matin et de l'après-midi, et correspond à un taux de blocage faible ; l'autre concerne la pointe du soir, provoquée par le trafic résidentiel, et correspond à un taux de blocage plus élevé. Le trafic d'affaires et le trafic résidentiel n'ayant pas la même répartition géographique, leurs matrices de trafic sont différentes. Le dimensionnement du réseau se fait en deux fois, d'abord de façon à satisfaire la demande d'affaires, puis en tenant compte du trafic résidentiel. Les taux de blocages sont établis de façon à minimiser le coût tout en fournissant une qualité de service socialement admissible. L'arbitrage entre ces deux objectifs est fait de façon empirique.

Le dimensionnement des routes suit une démarche analogue ; il part d'une mesure du trafic prévisionnel, les périodes de pointe se situant selon les artères considérées le matin et le soir (trafic pendulaire domicile travail dans les régions urbaines), ou pendant les vacances d'été (régions touristiques).

2. Caractère aléatoire de la demande

Des modèles prévoient la demande adressée à un réseau à un instant donné en fonction des facteurs qui l’expliquent. Ces modèles sont probabilistes : même si l'incertitude est limitée par la prise en compte de tous les facteurs explicatifs, la demande est aléatoire par nature. Le modèle fournit ainsi non la prévision de la demande, mais celle des paramètres d'une loi statistique à laquelle la demande se conforme à chaque instant (il s'agit le plus souvent d'une loi de Poisson, qui peut être approchée par une loi de Laplace-Gauss).

Supposons :

(2) que le réseau soit dimensionné de sorte que le taux de blocage soit inférieur à p ;

(3) que la demande totale sur le réseau soit proportionnelle à m.

Pour répondre à (2), le réseau doit être capable de transporter D_c telle que :

soit

t est fonction décroissante de p. Comme p est notoirement inférieur à 50 %, t > 0.

Le coût du réseau peut être approché au premier ordre par une fonction affine de son dimensionnement, soit d'après (4)

La recette rapportée par le réseau peut être approchée au premier ordre par une fonction affine du trafic total, soit d'après (3)

R = c + d.p.m, avec d > 0,

où p est le prix moyen du trafic.

Le profit est donc :

Il en résulte que :

Un accroissement de l'incertitude sur la demande provoque une diminution du profit apporté par l'exploitation du réseau, parce que pour assurer un trafic égal le réseau doit être dimensionné plus largement.

3. Économie du dimensionnement

L’économie d’un réseau n’est qu’à demi " à coût fixe ". Pour la représenter de façon simple, nous supposerons, en prenant l'exemple du transport aérien :

• Que le coût de dimensionnement est fonction linéaire de la dimension D du réseau, mesurée par exemple par le nombre de sièges*kilomètres offerts (SKO), ou encore en pondérant les SKO selon le type de l’avion et la longueur des escales, mais peu importe ici.
• Que le coût d’exploitation est un coût fixe, indépendant jusqu’au seuil D du nombre de passagers*kilomètres transportés (PKT), et qu’il devient infini si le nombre de PKT dépasse D (cela revient à supposer qu'il est impossible d'affréter des avions supplémentaires en cas de besoin, hypothèse que l'on peut juger forte ; nous y reviendrons)

On peut utiliser le même schéma pour représenter le coût d'un réseau de télécommunications : ce coût dépend de la capacité du réseau à acheminer un nombre D de communications. Une fois le réseau dimensionné, le coût a été payé, et il sera le même quel que soit le nombre de communications pourvu qu'il soit inférieur ou égal à D. Le réseau est incapable d'acheminer davantage de communications (les appels supplémentaires sont refoulés), et donc le coût d'exploitation de court terme est infini au delà de D. Un raisonnement analogue peut être fait sur le dimensionnement d'un réseau routier, d'un réseau de transport maritime, d'un réseau d'adduction d'eau, d’un réseau de distribution etc.

Dans le coût de dimensionnement on compte le salaire des personnels nécessaires pour faire fonctionner les installations, et donc pas seulement le coût d'investissement en capital fixe.

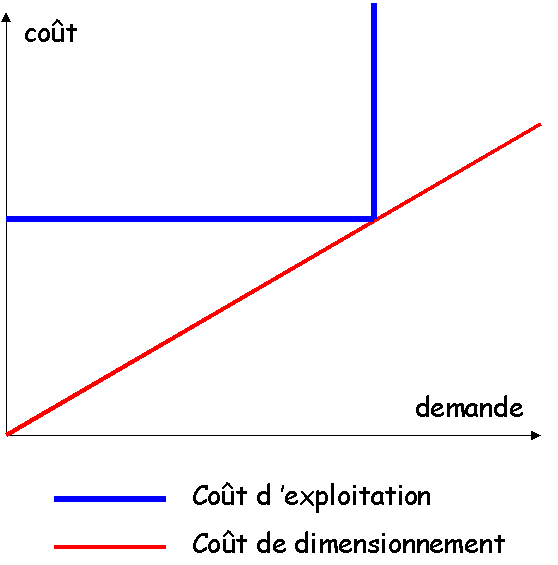
On peut alors représenter la fonction de coût en associant deux fonctions :

• coût de dimensionnement, mesuré par a, équivalent quotidien (en valeur actualisée) du coût unitaire des investissements et des frais de personnel nécessaires au dimensionnement : C = aD
• coût d’exploitation (quotidien) : c est égal à C si la demande est inférieure à D, c est infini si la demande est supérieure à D.

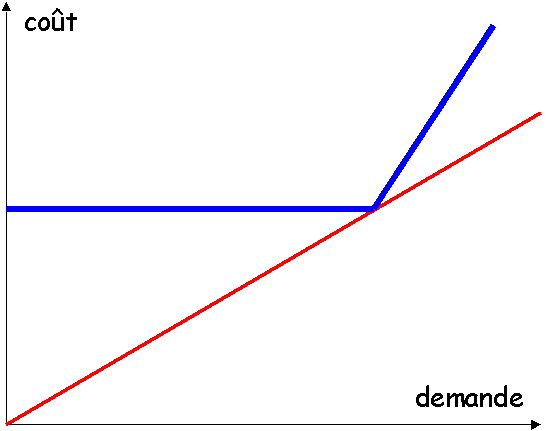
Il se peut que le coût d'une offre supplémentaire au dimensionnement soit élevé, mais non infini ; dans ce cas, l'on a au delà du seuil D un coût représenté par une demie droite de pente élevée. Ce sera le cas d’un réseau de distribution commerciale dimensionné pour écouler un certain volume, mais dont on peut accroître le débit en embauchant des vendeurs supplémentaires :

Revenons au transport aérien. Nous supposerons que le transporteur exploite une ligne à fréquence quotidienne : prendre en compte la multiplicité des lignes, la structure en " hub and spokes ", les fréquences etc. n’apporterait rien au raisonnement que nous voulons construire ici (même si ces aspects ont par ailleurs une incidence notable sur les coûts). Nous supposerons par ailleurs infini le coût d’une offre supplémentaire au dimensionnement.

(1) f(x) = s ^-1 (2p)^{- 1/2} exp{ - (1/2)[(x – m)/s]²}

Si x_t < D, tous les passagers peuvent être transportés.

Si x_t > D, il faut renoncer à transporter une partie des passagers.

Calcul du nombre moyen de clients

Le nombre moyen M de passagers transportés est non pas m, puisque cette moyenne recouvre aussi les jours où x_t > D, mais, en notant F(x) la fonction cumulative de f(x) :

Posons :

G = mF(D) + H, avec :

Donc :

Et finalement :

Maximisation du profit

Cherchons le dimensionnement D* qui maximise le profit. La recette est proportionnelle au nombre de clients ; le profit est donc :

or

Le dimensionnement optimal D* est donc tel que :

(5) 1 – F(D*) = a / p

Cette équation a une et une seule racine en D* si a / p < 1. Comme f(D*) > 0, la dérivée seconde du profit est négative : il s’agit donc bien d’un maximum.

La position de D* par rapport à m dépend donc du rapport entre le coût unitaire du dimensionnement et le prix unitaire du billet :

• si a / p > 0,5, D* < m ;
• si a / p = 0.5, D* = m ;
• si a / p < 0,5, D* > m.

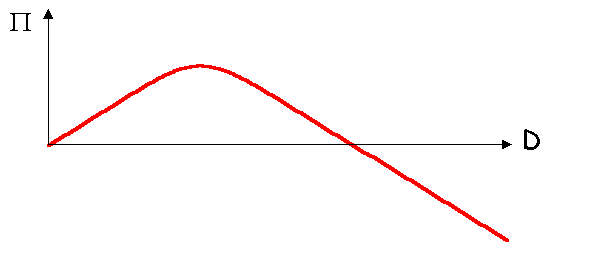
Le profit maximal est atteint pour D* = 10.

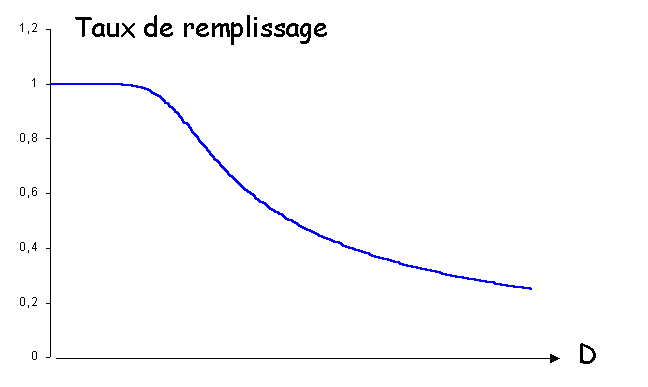
Le taux de remplissage moyen est de 92 % si D = D* = 10.

Considérons enfin l’effet du coût unitaire a du dimensionnement, en supposant p donné ; si a est nul, le dimensionnement optimal est infini ; si a augmente, le dimensionnement optimal diminue ; D* est nul lorsque a = p.

Dimensionnement optimum

Le dimensionnement a pour conséquence que certains clients ne sont pas servis. Supposons leur perte d’utilité égale à k fois le prix du service.

L’espérance mathématique du nombre de clients qu’il est impossible de satisfaire est B tel que :

d’après (2) :

(7) M = m - B + D[1 - F(D)]

d’où

Le surplus est alors :

Le surplus est maximal si le dimensionnement est D* tel que :

(10) 1 - F(D*) + kD*f(D*) = a/p

Le dimensionnement qui maximise le surplus est supérieur à celui qui maximise le profit, comme le montre le graphique ci-dessous où l’on a supposé k = 1 :

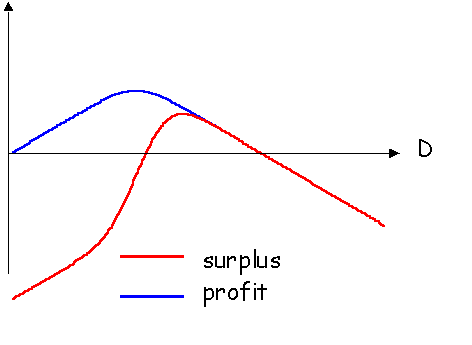
On retrouve ici un résultat classique : le dimensionnement qui maximise le profit du fournisseur en situation de monopole (ou de concurrence monopoliste), est sous optimal du point de vue du surplus social.

Eléments d’économie du " surbooking "

Un transporteur aérien doit gérer, outre le caractère aléatoire de la demande x_t, un autre aléa : celui de la réservation des places. En effet les passagers qui ont réservé ne se présenteront pas tous à l’enregistrement (" no-show "), et par contre certains passagers qui n’ont pas réservé se présenteront au dernier moment (" go-show "). L’espérance mathématique E(N) des no-show est supérieure à l’espérance E(G) des go-show. Si le transporteur s’interdit de réserver plus de places qu’il n’y a de sièges disponibles dans l’avion, son taux de remplissage moyen 1 - E(N) + E(G) sera inférieur à un, alors que la demande aurait permis de remplir l’avion.

Il est donc intéressant pour lui de prendre plus de réservations qu’il n’y a de places dans l’avion. Cependant il encourt alors le risque de mécontenter des passagers qui ont réservé et qui ne peuvent pas embarquer dans l’avion. Il faut les dédommager de telle sorte qu’il n’y ait pour le transporteur ni perte d’image, ni perte de fidélité.

Soit X la demande pour un vol, Y la demande de réservation, D le nombre de sièges de l’avion. Le couple (X, Y) est aléatoire. On peut supposer que sa distribution suit une loi normale bi-dimensionnelle, que Y et X sont corrélés positivement, et que l’espérance conditionnelle de Y pour une valeur donnée de x est inférieure à x :

La connaissance de Y apporte donc une information sur X, car la variance conditionnelle de X est inférieure à sa variance inconditionnelle ; cette information est d’autant plus importante que la corrélation entre X et Y est plus élevée.

Supposons que le transporteur ait pour politique de déclarer l’avion complet une fois qu’il a réservé T sièges, avec T > D. D’une part il perd définitivement les recettes apportées par les passagers qui se présentent lorsque l’avion est déclaré complet ; et il existe une probabilité que les sièges de l’avion ne soient pas tous occupés en raison du phénomène de no-show. D’autre part, ayant réservé plus de sièges que l’avion n’en comporte, il risque de se trouver dans une situation où l’avion sera plein, mais où certains passagers auront été " surbookés " ; il faudra leur offrir une compensation égale à un multiple k du prix du billet. Il faut choisir la politique qui maximise le profit tout en arbitrant entre ces divers risques.

Un calcul complet doit tenir compte de la possibilité de reporter un passager d’un vol vers un autre, notamment dans les systèmes à fréquence élevée comme les navettes : dans ce cas, la recette apportée par ce passager n’est pas perdue, sauf s’il se reporte vers un vol d’un concurrent.

4. Diversification des services sur un réseau

Chaque réseau s'est construit autour d'un service de base (télécommunications, énergie, transport), auquel peuvent être associés des services complémentaires, ou " services à valeur ajoutée ".

On peut comparer la mise en valeur d'un réseau à celle d'une propriété foncière. L’entreprise qui pratique une politique " latifundiaire " se concentre sur l'acquisition d'une part de marché importante pour le service de base et néglige les possibilités de diversification qu'apportent les services à valeur ajoutée. Elle tend naturellement au monopole.

Si ce monopole est rompu, d'autres exploitants se créent sur le marché du service de base : une guerre des prix se déclenche entre les latifundiaires et les nouveaux entrants, comme l’a montré l'histoire des réseaux des télécommunications et du transport aérien aux États-Unis).

Alors le service de base ne présente plus à moyen terme de perspective de profit, et la priorité donnée à la part de marché sur ce service devient un piège. La politique doit évoluer : le service de base sera considéré comme une plate-forme de marketing qui doit attirer le client, le profit étant attendu des services à valeur ajoutée produits sur cette plate-forme.

Les opérateurs télécoms offriront des réseaux privés virtuels, des accès à l’Internet, l'hébergement de serveurs Web, des conférences téléphoniques, des " call centers ", des services de renseignement, des messageries vocales, des services autour de la messagerie, des bases de données, des bases documentaires, des cartes à mémoire, de l'administration de contrôle d'accès, de la sécurité des transactions, etc. Les transporteurs aériens offriront des prestations autour du voyage : réservation de chambres d'hôtel et de voitures, vente à bord, télévision, revues et journaux, télécommunication à bord (téléphonie, données), mise à disposition de radio-téléphones en escale, etc.

Tous les opérateurs de réseau offrent ou vont offrir en outre aux grandes entreprises des éléments de comptabilité analytique en présentant leurs factures sous le format et sur le support demandé par le client en retraitant les informations recueillies à l'occasion du service (dépenses faites par les salariés en voyage, etc.).

D'autres formes de différenciation, plus étroitement liées au transport, se présentent dans le transport aérien : différenciation des classes à l'intérieur d'un même vol, multiplication des fréquences. Ce dernier point mérite un bref commentaire. Pour acheminer un nombre donné de SKO entre deux points, l'avion le plus gros sera le moins coûteux ; si l'on cherche cependant à maximiser non la capacité de transport, mais le profit, il sera souvent plus efficace de mettre en fonction des avions plus petits, plus nombreux, dont les horaires se répartissent sur toute la journée. En effet, tout passager a un horaire idéal, celui qui convient le mieux à ses contraintes personnelles ; l'utilité du vol est fonction décroissante de l'écart entre l'horaire offert et l'horaire idéal. En répartissant des vols tout au long de la journée, le transporteur diminue en moyenne l'écart entre horaire offert et horaire idéal et accroît l'utilité de son offre pour le passager ; il drainera ainsi une demande supérieure.

Segmentation tarifaire (" Yield management ")

Les transporteurs aériens ont inventé le " Yield management " (ou " Revenue management ") qui consiste à chercher à vendre à chaque client juste au-dessous du prix maximum que celui-ci serait prêt à payer. Cette politique correspond bien à la fonction de coût du transport aérien : une fois que les premiers passagers ont payé le prix qui équilibre le coût d'un vol, les derniers sièges restants peuvent être vendus à un prix aussi bas que l'on voudra, ils rapporteront toujours du profit.

Ici s'introduit une possibilité de différenciation qui complète et complique le modèle classique de concurrence monopoliste. Dans le modèle usuel, on suppose que le prix du produit vendu est fixe quel que soit le client. La segmentation tarifaire incite par contre à pratiquer une tarification personnalisée.

Si certains des clients d’un opérateur de réseau (transport aérien, télécoms etc.) risquent de passer à la concurrence (c'est le cas des communes ou des grandes entreprises pour les télécoms, des clients résidant dans des villes périphériques éloignées du " hub " pour le transport aérien, etc.), il sera toujours possible, sans pour autant afficher des prix unitaires différents, de conclure avec eux des accords comportant une ristourne en fin d'année, et de la personnaliser au plus juste en fonction du risque de concurrence.

Partenariats et alliances

L'exploitant d'un réseau améliore son offre - donc sa compétitivité - en concluant des partenariats avec d'autres exploitants. Ces alliances entre entreprises naturellement concurrentes sont souvent instables : dans le transport aérien, peu de partenariats ont duré plus de deux ans.

Les exploitants de télécoms offrent implicitement l'interconnexion de leurs réseaux. Au début de l'histoire du téléphone, les réseaux n'étaient pas interconnectés, et un homme d'affaires qui voulait pouvoir contacter des correspondants abonnés à divers réseaux devait avoir autant de téléphones. L'interconnexion générale des réseaux, dont la contrepartie réside dans un système de comptabilisation et compensation des redevances entre exploitants, a mis fin à cette situation incommode.

Des partenariats sont passés entre transporteurs aériens pour limiter les frais commerciaux ; les apports de trafic sont rémunérés par des primes (" inter line "). Le " code sharing " partage les sièges d'un même vol entre plusieurs compagnies de sorte que le même vol apparaît sous plusieurs identifiants sur les écrans des systèmes de réservation. Le passager a pris un billet Air France de Paris à Seattle, mais en fait il changera d'avion à New York et empruntera un vol de Delta. Certains passagers trouvent cette pratique choquante, d'autres y sont indifférents, mais le transporteur qui augmente la panoplie de ses O&D présentées sur les systèmes de réservation accroît d’autant sa chance de drainer du trafic.

Risques de rigidité

La diversification de l'offre n'est pas toujours la politique que les opérateurs de réseau choisissent d'abord. Lorsque la concurrence s'avive, leur premier réflexe est de se replier vers leur cœur de métier, car ils s’y croient en position de force. Cela revient parfois à pratiquer la politique que résume la phrase célèbre : " je vends au-dessous du coût de revient, mais je me rattrape sur la quantité ".

C'est ainsi que des transporteurs aériens ont, alors que les tarifs s'effondraient, massivement investi pour maintenir le niveau de leur flotte, de leurs " SKO " (sièges kilomètres offerts), dans l'espoir de protéger leurs parts de marché en volume. C'est ainsi que des opérateurs télécoms ont lancé une politique de promotion du trafic (le " delta minutes "), alors que le prix du trafic baissait.

De telles politiques ont souvent la faveur des directions générales à qui elles permettent de mobiliser l'entreprise autour d'un objectif correspondant à sa culture (quand on est sur la défensive le premier réflexe est de mobiliser les troupes) ; et l'évolution d’un volume semble plus tangible que l'évolution d’un prix. Par contre la diversification des services, corollaire nécessaire de l'ouverture de la concurrence sur un réseau, est difficile pour un opérateur traditionnel. Il ne pourra s'y lancer qu'à l'issue d'une " révolution culturelle " accompagnée du renouvellement de l'équipe dirigeante.

La rigidité des conceptions professionnelles étonne dans des secteurs qui se sont développés autour de techniques nouvelles. L'histoire éclaire ce paradoxe. Les innovations ont été réalisées par de petites équipes de pionniers ; ces équipes se sont dispersées lorsqu'il a fallu consolider l'exploitation commerciale. Leurs " héritiers " ont utilisé les résultats des pionniers sans toujours percevoir les intuitions dont ils résultaient. Des choix techniques ou commerciaux, provisoires et fluides chez les pionniers, sont devenus des dogmes chez leurs successeurs. Ces dogmes, imposés par des arguments d'autorité, sont devenus aussi rigides que du béton armé.

Effet d'avalanche

L'économie des réseaux de télécommunications est caractérisée par l'effet d'avalanche : comme l'utilité du réseau dépend du nombre de correspondants qu'il relie, cette utilité est fonction croissante du nombre des utilisateurs raccordés. 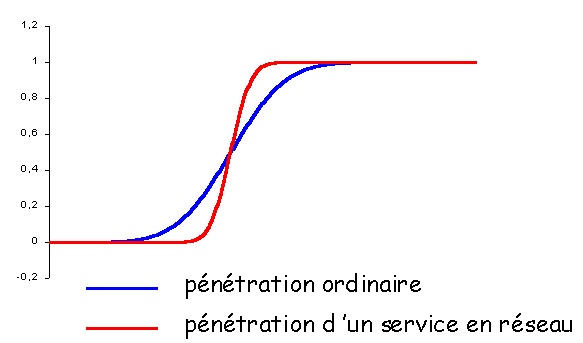Lorsque l'exploitation d’un réseau démarre, il sera peu attractif parce que le nombre de personnes raccordées est faible ; puis lorsqu'un seuil de pénétration critique est atteint son utilité devient assez élevée pour que tout le monde souhaite être raccordé. La courbe en S qui caractérise la pénétration d'un service est donc dans le cas du réseau de télécommunications particulièrement plate au début, puis particulièrement pentue par la suite.

Un effet analogue se produit pour les services à valeur ajoutée : si l'on ouvre dans une entreprise un service de messagerie, une documentation électronique, un agenda partagé, ils resteront peu utilisés pendant un temps, et tout le monde voudra les utiliser lorsqu'ils auront atteint la pénétration critique.

Il existe d’ailleurs une externalité croisée entre un réseau et les services offerts au dessus de lui. Plus le nombre d'utilisateurs du réseau est élevé, plus l'offre de services est active, un nouvel offreur pouvant espérer trouver sur un réseau bien distribué le nombre de clients nécessaire (cf. le Minitel et l'Internet). Par ailleurs, le raccordement au réseau est d'autant plus attirant que les services offerts sont plus diversifiés. Ici s'enchaîne un autre mécanisme de croissance, les aspects réseau et service se soutenant mutuellement.

Le transport aérien suscite un phénomène analogue, quoique moins brutal, l'ouverture d'une ligne pouvant faciliter la coopération économique entre des escales.

Le management des entreprises de réseau comporte donc une difficulté particulière : comment gérer l'effet d'avalanche, garder la tête froide pendant la phase d'attente, détecter les signes avant-coureurs de l'avalanche pour préparer le dimensionnement et éviter que la file d'attente des utilisateurs ne s'allonge démesurément ?

5. Exemples de fonctions de coûts

Nous présenterons dans les chapitres suivants les fonctions de coût des télécommunications, du transport aérien et de l’Internet.

Dans ces trois cas, la fonction de coût est fondée sur une économie du dimensionnement : en partant d'une demande anticipée (donc incertaine), et en utilisant des règles d'ingénierie consacrées par la pratique professionnelle et tenant compte de la nature aléatoire du trafic, le réseau est dimensionné pour garantir en heure de pointe une qualité de service jugée acceptable.

Le coût de l'offre est donc un coût de dimensionnement, payé pour partie une fois pour toutes lors de la mise en place des équipements, pour partie au fur et à mesure de l'exploitation. Il dépend peu du trafic effectivement acheminé : qu'un avion soit plein ou vide, le coût pour le transporteur aérien sera à peu près le même.

Nous allons, dans les trois cas, suivre la même démarche de modélisation : on construit les réseaux par simulation en partant d'hypothèses sur la demande à satisfaire et d'une connaissance des règles d'ingénierie.

Le réseau Internet est totalement maillé, son coût est proportionnel à sa taille (et à l'intensité du trafic qu'il achemine). Sa pérennité résulte de la simplicité des composants qu'il utilise et de la baisse tendancielle de leur coût.

Le réseau de télécommunications bénéficie de l'économie d'échelle procurée par la commutation et la concentration du trafic sur les faisceaux de transit, la contrepartie de cette économie d’échelle résidant dans le blocage en heure de pointe.

Les transporteurs aériens ont mis en place des structures proches de celles des réseaux de télécommunications. La plupart retiennent en effet, pour acheminer au moindre coût le trafic entre origine et destination (O&D), une structure de réseau en " hub and spokes " analogue à celle des télécoms avec les commutateurs. Ils peuvent ainsi, pour un coût d'exploitation donné, multiplier le nombre des couples O&D commercialisés.

La connaissance de Y apporte donc une information sur X, car la variance conditionnelle de X est inférieure à sa variance inconditionnelle ; cette information est d’autant plus importante que la corrélation entre X et Y est plus élevée.

Supposons que le transporteur ait pour politique de déclarer l’avion complet une fois qu’il a réservé T sièges, avec T > D. D’une part il perd définitivement les recettes apportées par les passagers qui se présentent lorsque l’avion est déclaré complet ; et il existe une probabilité que les sièges de l’avion ne soient pas tous occupés en raison du phénomène de no-show. D’autre part, ayant réservé plus de sièges que l’avion n’en comporte, il risque de se trouver dans une situation où l’avion sera plein, mais où certains passagers auront été " surbookés " ; il faudra leur offrir une compensation égale à un multiple k du prix du billet. Il faut choisir la politique qui maximise le profit tout en arbitrant entre ces divers risques.

Un calcul complet doit tenir compte de la possibilité de reporter un passager d’un vol vers un autre, notamment dans les systèmes à fréquence élevée comme les navettes : dans ce cas, la recette apportée par ce passager n’est pas perdue, sauf s’il se reporte vers un vol d’un concurrent.