|
Chapitre IV : Concurrence monopoliste
(extrait de Michel
Volle, e-conomie, Economica 2000)
La théorie de la concurrence monopoliste vise à
expliquer :
- en ce qui concerne les producteurs, la différenciation des
produits ;
- en ce qui concerne les consommateurs, le choix entre
variétés d'un même produit.
Cette théorie, formulée pour la première fois par E. H.
Chamberlin, a fait l'objet dans les années 70 d'une abondante littérature. Elle joue,
entre les deux extrêmes du monopole et de la concurrence parfaite, le rôle d’une
charnière. Cette position centrale, qu'elle partage avec la théorie de l'oligopole et la
théorie des jeux, lui confère à la fois une grande richesse et une certaine
complexité. Ses applications, toutes d'ordre théorique, simulent le fonctionnement de
certains marchés à l'aide de petits modèles simplifiés. Elle a donc un pouvoir
d'explication et d'élucidation des mécanismes plutôt que de prévision chiffrée. Ses
applications économétriques restent rares.
Nous allons décrire la concurrence monopoliste en considérant
d'abord le côté du producteur, puis celui du consommateur. Avant d'entrer dans le
formalisme de la théorie, nous allons l'illustrer à partir d'un exemple.
1. Un exemple simple
Considérons le marché du béton prêt à l'emploi. Certes on
est loin avec cet exemple des nouvelles technologies et du STC, et pourtant il permet une
première approche de la forme de leur marché.
Une centrale à béton est un équipement simple où sont
mélangés les ingrédients du béton (ciment, sable, gravier, eau). Les camions des
entrepreneurs en bâtiment et travaux publics (les " toupies ")
s'approvisionnent au pied de cet équipement.
Pour le client, le coût de la tonne de béton livrée sur le
chantier est la somme du prix a de la tonne payée à la centrale et du coût de
transport, ce dernier étant élevé car la valeur du kg de béton est faible (c’est
un " bien pondéreux "). Si nous notons b le coût de la
tonne*kilomètre, le coût de la quantité q livrée sur le chantier est :
(1) c(q) = (a + b.d)q,
où d la distance en km entre le chantier et la centrale.
Supposons que deux centrales soient installées dans la même
zone géographique, et qu'elles pratiquent le même prix a. Un chantier
s'approvisionnera à la centrale dont il est le plus proche. Le marché est donc divisé
en deux selon la médiatrice du segment qui joint les deux centrales. Pour les chantiers
situés sur cette frontière, les deux centrales sont équivalentes.
Le graphique ci-dessous représente le coût de la tonne en
fonction de la localisation x du chantier, en supposant que l'on se trouve dans un espace
à une dimension. La frontière est située au point F. À droite de F l'entrepreneur
choisit la centrale C2, à gauche il choisit C1.
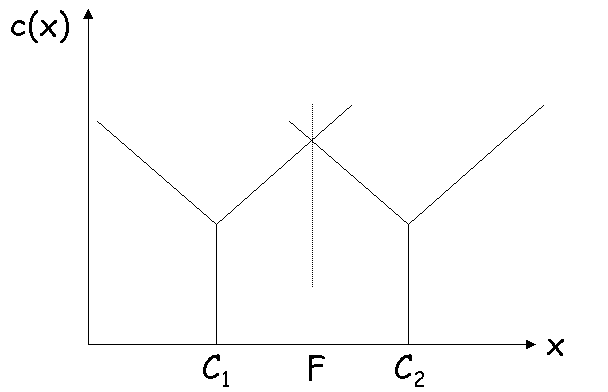
Supposons que la centrale C2 baisse son prix. Dans ce
cas, la frontière se déplace, et le territoire de la centrale C2 s'élargit.
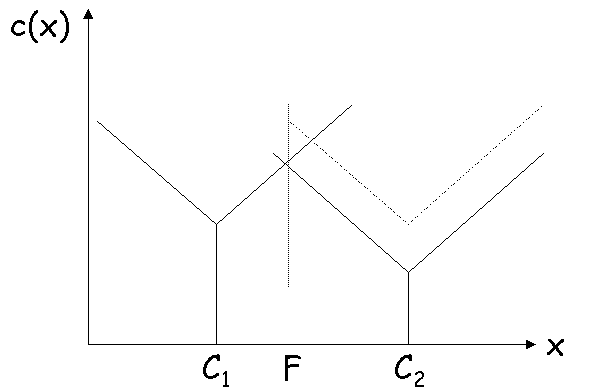
Ceci explique l'appellation " concurrence monopoliste
" : une centrale est en situation de monopole envers les chantiers situés à
l'intérieur de son territoire, et en situation de concurrence sur la frontière de son
territoire. Elle peut agrandir son territoire en diminuant son prix, ce qui entraîne un
déplacement de la frontière.
Supposons que le marché obéisse aux conditions
suivantes :
- la fonction de coût de la centrale à béton est à rendement croissant (c'est
en effet le cas en pratique),
- la densité des chantiers de BTP est uniforme (homogénéité du territoire),
- le quadrillage des routes est uniforme (isotropie du territoire),
- les centrales se créent librement.
À l'équilibre, les centrales vendent au prix qui couvre leur
coût de production (plus la prime de risque jugée normale sur le marché considéré).
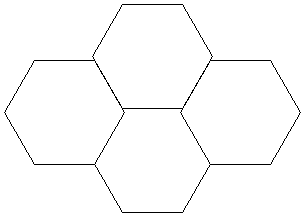
Le territoire est découpé en hexagones, desservis chacun par une centrale située en son
centre. Une centrale est en situation de monopole à l'intérieur de l'hexagone qu'elle
dessert, de concurrence sur la frontière de l'hexagone. Le nombre de centrales est une
endogène dépendant de la densité de la demande et de la fonction de coût d'une
centrale : plus la demande est forte, ou plus le coût de production est bas, plus les
hexagones sont petits et le nombre de centrales élevé.
2. Leçons à tirer
Nous allons généraliser l'exemple ci-dessus, et lui donner une
portée plus large que le modèle géographique que nous avons considéré. Puis nous
préciserons sa portée, en délimitant les cas où un équilibre de ce type se présente
naturellement. Enfin, nous décrirons les relations entre ce type d'équilibre et le
" style " de l'économie.
Généralisation
La représentation géographique ci-dessus peut s’étendre
à des espaces abstraits. Considérons le marché d'un bien susceptible de
différenciation (marché des services d'information, des automobiles, des cravates, etc.)
et dont la fonction de coût est à rendement croissant. Situons ce marché dans un espace
tel que chaque caractéristique du bien soit représenté par un axe, et que chaque
consommateur soit situé au point qui représente ses besoins. L'utilité du produit pour
le consommateur est maximale si on lui offre la variété correspondant exactement à son
besoin, et plus basse (mais non nulle) si on lui offre une autre variété, la perte
d'utilité étant fonction d'une "distance " entre variété " idéale
" et variété offerte.
L'équilibre d'un tel marché peut se décrire comme celui des
centrales à béton : chaque consommateur choisit la variété la plus proche de sa
variété idéale, et le " territoire " abstrait des besoins est pavé
d'alvéoles correspondant chacune à la zone de monopole d'une variété. Le nombre de
variétés offertes sera une endogène dépendant de la densité des consommateurs et de
la fonction de coût d’une variété.
Cette représentation peut rendre compte aussi des cas où les
besoins d'un consommateur varient dans le temps (c'est le cas des services d'information,
car un consommateur peut avoir besoin d'informations diverses selon le moment : il
consulte alternativement l'annuaire téléphonique, les horaires de trains, l'agenda des
spectacles, etc.) Dans ce cas, le point qui représente un consommateur se déplace dans
l'espace, mais l'équilibre reste inchangé si les déplacements des divers consommateurs
se compensent statistiquement.
Coûts fixes et concurrence monopoliste
Pour situer la concurrence monopoliste, rappelons quelques
résultats élémentaires relatifs à la concurrence parfaite et au monopole.
Considérons un bien homogène dont la production est réalisée
par des entreprises ayant toutes la même fonction de coût. Nous
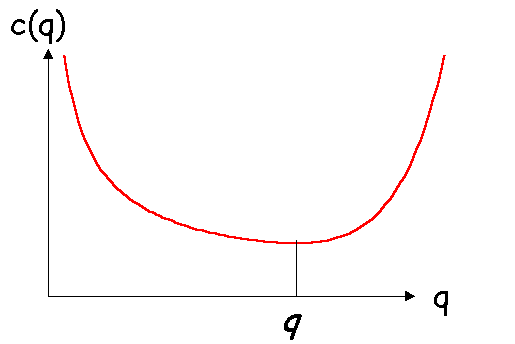
supposons les rendements d'abord croissants, puis décroissants. Le coût moyen est :
(2) c(q) = c(q)/q
Il passe par un minimum pour le niveau de production q.
Concurrence parfaite
Notons
(3) p = D(Q)
la fonction de demande, où Q désigne la quantité vendue sur
le marché.
Si la demande porte sur des quantités très supérieures à q,
on est dans une situation concurrentielle : les entreprises sont nombreuses sur
le marché ; le prix est pour chaque entreprise une variable exogène qui s'impose à elle
de l'extérieur (l'accroissement de l'offre provenant d'une augmentation de la quantité
produite par une seule entreprise serait trop faible pour faire baisser le prix
d'équilibre). Dans ces conditions, le profit P d'une entreprise produisant la quantité q est :
(4) P = pq
- c(q),
d’où :
(5) d P /dq
= p - c'(q)
Le profit sera maximal si l'entreprise vend au coût marginal.
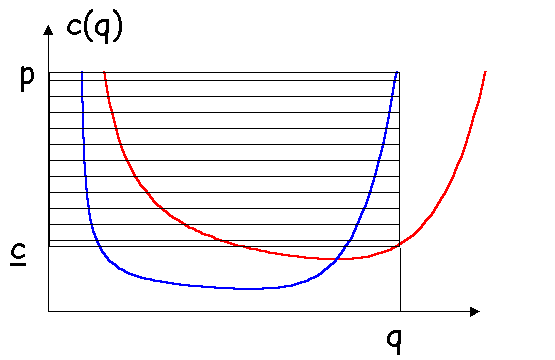
On obtient la fonction d'offre globale en multipliant l'abscisse
de la courbe des coûts marginaux par m, où m est le nombre des entreprises produisant le
bien considéré.
(6) p = O(Q) = c'(Q/m)
Supposons qu'il y ait libre entrée sur ce marché. La
possibilité de faire du profit provoque la création de nouvelles entreprises, donc une
augmentation de l'offre qui entraîne une baisse du prix d'équilibre.
Lorsque le processus arrive à son terme, le prix de vente est
égal au minimum de c. Chaque entreprise produit q, ce qui correspond
à l'efficacité maximale (minimum du coût moyen de production). Le profit est nul pour
chaque entreprise. Le nombre des entreprises présentes sur le marché est:
m = Q/q,
où Q est la quantité du bien demandée pour le prix p
= c(q) :
Q = D-1[c(q)]
Monopole naturel
Si la demande porte sur des quantités inférieures à q,
on est dans une situation de monopole naturel :
en effet, comme pour q < q le coût moyen de production est décroissant,
une entreprise peut accaparer tout le marché et dissuader toute concurrence car
comme elle est a priori la plus grande elle a des coûts de production plus bas que les
autres.
L’entreprise en position de monopole n’est pas
confrontée à un prix exogène, mais à une fonction de demande. Son profit est :
P = q p(q) - c(q) = R(q) - c(q),
où R(q) est la recette obtenue lorsque l'on met en vente la
quantité q.
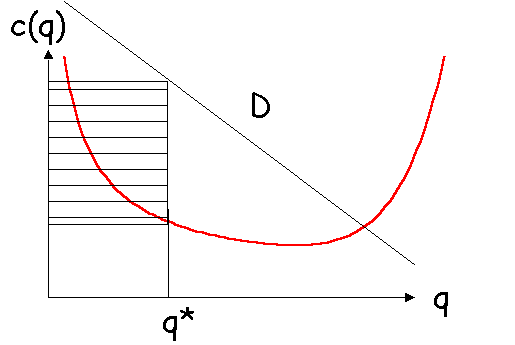
d P /dq =
R' - c'
- Le niveau de production q* qui maximise le profit est tel que
la recette marginale R’ égale le coût marginal c’ ; le profit est
alors :
P = (p - c)q*
Concurrence monopoliste
Considérons un bien dont le marché était en situation de
concurrence parfaite, et dont la fonction de production devient, en raison d’une
innovation, une fonction à rendement croissant. Le marché va s’organiser autour
d’un monopole.
Cependant les autres entreprises peuvent survivre si elles
peuvent différencier leur produit et découper ainsi, dans la demande globale, un
segment sur lequel elles auront un monopole. Elles substituent ainsi, au marché unique
sur lequel s'échangeait un produit indifférencié, des marchés distincts où chacune
écoule une (ou plusieurs) variété(s) du produit, correspondant chacune à un
segment de la demande.
Les produits ne se prêtent pas tous à la différenciation : il
existe des produits essentiellement homogènes pour lesquels on ne peut pas imaginer de
variétés (produits chimiques purs comme l'acide chlorhydrique, l'acide nitrique, le
lingot de cuivre, etc.). Les marchés de tels produits sont inévitablement soumis au
régime de concurrence, de monopole ou d’oligopole, selon la position relative de la
courbe de coût moyen d'une entreprise et de la courbe de demande, mais ils ne peuvent pas
donner occasion au régime de concurrence monopoliste.
Par contre beaucoup de produits se prêtent à la
différenciation. C'est le cas des automobiles, vêtements, machines outils, appareils
électroménagers, etc. Selon des procédés divers, qui vont de l'adaptation fine aux
besoins réels d'une partie de la population jusqu'à des manipulations de l'opinion par
des campagnes publicitaires créant des différenciations imaginaires, chaque producteur
se réserve alors une fraction de la demande sur laquelle il pourra pratiquer un prix de
monopole.
Supposons cependant que le produit se prête à une
différenciation illimitée et que l’entrée sur le marché soit libre. D'autres
producteurs vont lancer de nouvelles variétés, prenant ainsi une partie des clients des
variétés anciennes (nous regarderons de plus près ce processus lorsque nous examinerons
le comportement du consommateur). Les monopoles se font alors concurrence, chacun essayant
de capter le marché de l'autre.
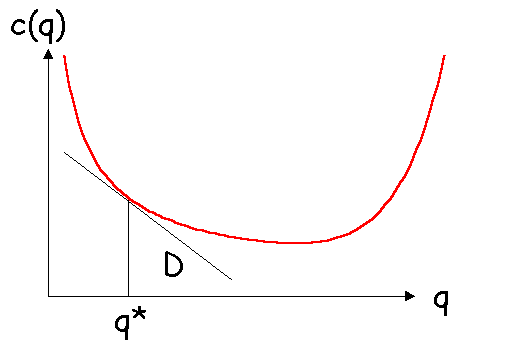
Ceci a pour effet de diminuer la demande adressée à chaque
entreprise (on suppose ici pour simplifier qu'une entreprise ne produit qu'une variété).
La courbe représentant la demande adressée à l’entreprise glisse progressivement
vers la gauche. La différenciation cesse que lorsque la courbe de demande est devenue
tangente à la courbe des coûts moyens.
Il s’agit bien d’un équilibre de monopole :
p’ = c’ = (c’ - c)/q et p = c
;
R’ = p’q + p = c’ - c + p = c’, cqfd
Dans ce cas, les profits de monopole eux-mêmes deviennent nuls.
On remarque cependant que q*< q et que p*> p : la
différenciation a conduit à une situation en un sens inefficace, puisque la production
ne se fait pas au minimum du coût moyen. Toutefois elle a permis de satisfaire les
besoins des clients de façon plus fine, et les produits sont plus utiles : le bilan en
termes d'efficacité ne s'apprécie donc pas d'une façon simple.
Monopole ou concurrence monopoliste ?
Dans une économie où toutes les entreprises ont une fonction
de production à coût fixe, chaque secteur se trouve en concurrence monopoliste ou en
situation de monopole.
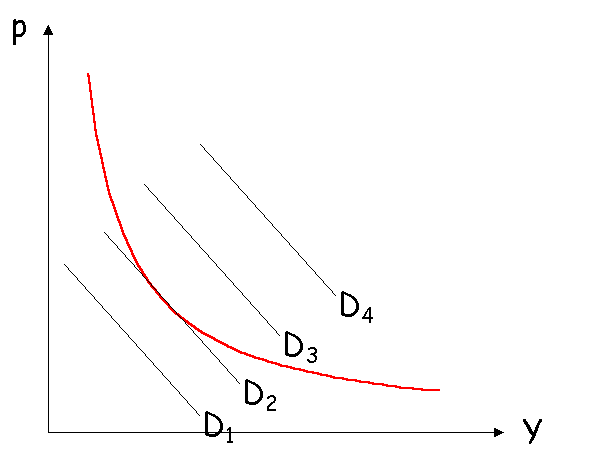
La forme de la concurrence dans le secteur est déterminée par
la situation relative de la fonction de demande et de la fonction de coût. Si la demande
est très faible, la courbe de demande passe au dessous de la courbe de coût moyen (qui
est ici un arc d’hyperbole), et il est impossible de créer une entreprise dans ce
secteur dont la production sera donc nulle. Si la courbe de demande est tout juste
tangente à la courbe de coût moyen, le secteur peut donner naissance à une entreprise
qui sera en position de monopole mais fera un profit nul.
Si la courbe de demande continue à glisser vers la droite, le
secteur sera en situation de monopole et ce monopole sera profitable. S’il n’y a
pas différenciation du produit, le monopole peut dissuader toute velléité
d’entrée sur le marché, car il est en mesure de lui riposter par une baisse de
prix.
Si la différenciation est possible, des entreprises peuvent
entrer sur le marché et concurrencer le monopole en produisant d’autres
variétés du produit : le produit n’étant pas identique, la dissuasion par le
prix n’a qu’un effet limité.
La différenciation a pour effet (a) d’accroître la
demande globale adressée au secteur, l’utilité moyenne du produit pour un
consommateur étant accrue par la différenciation ; (b) de diminuer la demande
adressée à une seule entreprise, puisque cette demande est relative non plus à la
totalité du produit, mais seulement à la variété fournie par cette entreprise.
S’il y a libre entrée, la différenciation se poursuit
jusqu’à ce que la demande adressée à chaque entreprise soit telle que le profit
soit nul.
Portée du modèle de concurrence monopoliste
La concurrence monopoliste est-elle fréquente ? Ce type
d'équilibre prévaut-il dans une part importante de l'économie ? Dans quelle condition
émerge-t-il ?
Dans le commerce international, les biens différenciés font
l'objet d'échanges croisés. La part prise par les échanges croisés dans les échanges
internationaux est un indicateur du niveau de la différenciation et de l'extension de la
part prise par la concurrence monopoliste dans les économies. Nous vérifierons son
importance au chapitre XIV.
Le passage du rendement décroissant au rendement croissant, et
notamment le passage à la fonction de production à coût fixe, cas extrême du rendement
croissant, entraîne, s'il est possible de différencier le produit, une différenciation
maximale de la production.
L'équilibre de concurrence monopoliste, ainsi que la
différenciation qui en est le corollaire, est donc conséquence endogène du changement
de technologie qui induit la fonction de production à coût fixe. La concurrence
monopoliste est la forme d'équilibre qui convient lorsque cette fonction de production se
généralise.
Robert Solow a proposé de reconstruire les fondements
théoriques de la macroéconomie en utilisant la concurrence monopoliste. Il est notoire,
dit-il, que si la microéconomie est théoriquement satisfaisante (cohérente, puissante
etc.), elle ne rend pas bien compte des faits observés ; la macroéconomie, plus
" réaliste ", a par contre le défaut d'être faible sur le plan
théorique. Tout cela vient du fait que la microéconomie privilégie le modèle de
concurrence parfaite, puissant, élégant mais irréaliste. Si l'on part du modèle de
concurrence monopoliste - plus compliqué, plus difficile, donc moins élégant, mais plus
réaliste - on peut construire une macroéconomie solide sur le plan théorique tout en
conservant ses qualités de réalisme.
La concurrence monopoliste permet en effet d'endogénéiser les
éléments essentiels de la théorie keynésienne :
- multiplicateur : un accroissement de
la demande entraîne une croissance du profit qui suscite un nouvel accroissement de
demande etc.
- prix rigides : l'incitation à
corriger une erreur de prix est plus faible en concurrence monopoliste qu'en concurrence
parfaite, et comme les révisions de prix comportent des inconvénients pratiques (pensez
à un restaurateur qui modifie son menu) les prix sont plus rigides que la concurrence
parfaite ne le suppose.
- quantités anticipées : en
concurrence parfaite, les prix constituent le seul signal dont les agents économiques ont
besoin ; en concurrence monopoliste, l'information utile concerne aussi les quantités,
puisque l'entreprise fixe son propre prix.
- chômage involontaire : si la fonction
de production était à rendement décroissant, il n'y aurait pas de chômeurs parce que
de petites unités employant une seule personne seraient compétitives : chaque chômeur
s'en sortirait donc en créant une entreprise. Le chômage involontaire implique qu'il
existe dans la fonction de production une zone initiale de rendement croissant qui
constitue une barrière à l'entrée pour les très petites entreprises.
- anticipations de long terme : sur un
marché où les entreprises offrent un produit diversifié, la " libre
entrée " des concurrents est risquée et difficile. A supposer que les
entreprises existantes fassent du profit, elles ne seront concurrencées par de nouveaux
entrants que si ceux-ci sont optimistes sur leurs chances de succès à long terme.
- équilibres inefficaces : Solow a
construit un petit modèle qui montre la possibilité de plusieurs équilibres dont
certains sont plus efficaces que d'autres. Il se peut alors qu'une économie reste
" collée " sur un équilibre inefficace car le pessimisme des acteurs
est auto-réalisateur.
" Style " de l'économie
Considérons un marché où la fonction de production est à
coût fixe et dont l'équilibre se fait sous le régime de la concurrence monopoliste.
La situation de l’entrepreneur sur ce marché est
périlleuse. D'une part, il doit payer la totalité du coût de production avant d'avoir
vendu une seule unité du produit, donc sur la base d'une anticipation de la réponse du
marché à son offre. Cette anticipation dépend de l'idée qu'il se fait de la demande
future.
Supposons que la fonction de demande soit de la forme :
D(p) = a - bp ;
si le producteur vend au prix unitaire p, sa recette sera
R(p) = ap - bp2, avec a, b > 0.
Il est donc possible de dégager un profit
P positif si, en notant c le coût fixe, il existe
des valeurs de p satisfaisant la condition :
P (p) = ap - bp2 - c > 0
Ce sera le cas si a2/4b > c.
Pour l’entreprise, la difficulté provient du caractère
incertain des paramètres a et b de la fonction de demande.
La demande adressée à l’entreprise dépend aussi des
offres futures des concurrents qui jouxtent le territoire (au sens de l'espace des
besoins) sur lequel elle souhaite détenir un monopole.
Supposons que le marché considéré soit en outre le théâtre
d'une innovation intense. Dans ce cas l'anticipation porte non seulement sur la demande et
l'offre des concurrents, mais sur leurs fonctions de coût : s'ils arrivent à trouver un
procédé qui réduit leur coût fixe, ils pourront se placer sur le segment visé par
l’entrepreneur en pratiquant un prix plus bas que les siens et rafler tout ou partie
de son marché.
Les facteurs d'incertitude sont donc nombreux. L'activité de
l'entrepreneur ressemble à un jeu de hasard où se succèdent des coups à quitte ou
double, et où les succès passés n'apportent aucune garantie pour le futur.
Dans une situation aussi dangereuse, il est naturel que
l’entrepreneur s'efforce de limiter les risques en pratiquant une politique de
partenariat. L'entente avec un concurrent stabilise la frontière avec ce concurrent et
permet de conjuguer les forces pour combattre les autres (notamment en associant les
moyens de recherche pour définir les produits et en alliant les forces commerciales).
D'autres partenariats peuvent être formés avec des entreprises apportant au produit des
qualités complémentaires. La pratique des partenariats est endogène à l'économie à
coût fixe. Le jeu de go, avec ses tactiques d'acquisition de territoire et
d'encerclement, illustre bien la logique de cette économie.
Le partage des territoires, les guerres de frontières, les
partenariats, rappellent l'économie de l'époque féodale, lorsque chaque seigneur, grand
propriétaire foncier, contrôlait un territoire autour de son château-fort, entretenait
la guerre sur ses frontières, et passait avec ses voisins ou son suzerain des accords
sanctionnés par des serments d'autant plus solennels qu'ils étaient bientôt violés. Il
est intéressant d'observer, au sein de l'économie la plus moderne, celle du STC, la
résurgence d'un style économique que l'on pouvait croire révolu. Le risque extrême,
associé en cas de réussite à des profits démesurés, suscite des formes de concurrence
violentes. Les entrepreneurs sont tentés de corrompre les acheteurs pour s'assurer des
débouchés, et pour cela il leur faut constituer des " caisses
noires " illégales. L'économie du STC donne donc du travail à l'appareil
judiciaire : les " affaires " lui sont endogènes.
Consommation
Supposons que sur le marché d'un produit le consommateur trouve
plusieurs variétés différentes (choix entre plusieurs types de pâtes dentifrices,
d'automobiles etc.). La réponse intuitive est immédiate : il choisira le produit
présentant le meilleur rapport qualité/prix. Peu importe ici que la mesure de la
qualité soit " objective " ou " subjective ", qu'elle découle de
différences réelles des variétés ou des images créées par la publicité.
Si le prix d’une variété s’élève, elle perd des
clients, mais continue tout de même à se vendre : c'est l'un des
effets de la différenciation. Si le produit était indifférencié, toutes les
entreprises seraient contraintes à vendre au même prix, car seule l'entreprise qui vend
au prix le plus bas pourrait écouler sa production. Mais ici, comme le produit est
différencié en variétés à chacune desquelles correspond un segment distinct du
marché, la hausse du prix d'une variété n'entraîne pas sa disparition complète.
Ce modèle explique les échanges croisés : chaque pays se
spécialise dans la production de certaines variétés, et ses consommateurs se
répartissent entre tous les segments correspondants à l'ensemble des variétés
produites dans le monde.
La différenciation des produits a pour effet d'amortir
l'incidence des mouvements de prix (et de parité) sur les échanges : dans le cas d'un
produit non différencié, et si le coût relatif du transport est bas, les achats se
réorientent d'une manière brutale, l'offreur qui pratique le prix le plus bas sur le
marché mondial raflant toutes les commandes. D'où le caractère instable des marchés
des matières premières, et la difficulté pour un pays producteur de prévoir la demande
et de planifier ses investissements (surtout lorsque les coûts de production dépendent
d'un facteur aléatoire comme le climat). Par contre, dans le cas de produits
différenciés, la hausse du prix entraîne certes une baisse des quantités, mais non
l'éviction totale du producteur du moins jusqu’à une certaine limite.
Annexe 1 du chapitre IV : Consommation d’un bien
diversifié
Supposons que l'ensemble des variétés possibles soit
représentable de façon continue dans un espace à une dimension, par exemple sur un
segment de droite de longueur 1. Si on suppose de plus les variétés 0 et 1 identiques,
on sera conduit à utiliser une représentation circulaire.
Considérons un consommateur dont la variété " idéale
" est v ; soit ½ v - v½
la longueur de l’arc joignant les variétés v et v.
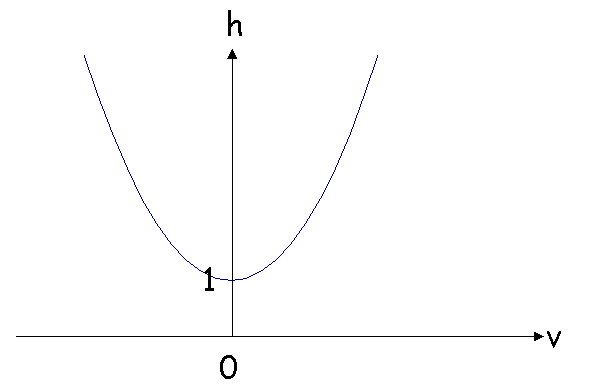
Supposons que pour ce consommateur la satisfaction apportée par
une unité de v soit égale à la satisfaction apportée par h(v - v)
unités de v, la fonction h ayant les propriétés suivantes :
h(0) = 1
h(x) = h(-x)
h(x) > 1 pour x ¹ 0
dh/| dv|
> 0
d2h/dv2 ³ 0
Supposons que v = 0 pour simplifier les notations. Soit
p(v) le prix de la variété v. Le rapport qualité/prix associé à v est
Q(v) = 1/h(v)p(v)
Le consommateur choisit parmi les variétés offertes sur le
marché celle qui minimise h(v)p(v) (cette quantité représente le prix à payer, si l'on
choisit v, pour obtenir une satisfaction égale à celle que procure une unité de v).
Considérons un consommateur qui utilise deux produits : X, bien
différencié, et Y non différencié. Le problème de ce consommateur est de
maximiser :
U(x,y) = U [x(v)/h(v), y]
sous la contrainte :
p(v)x(v) + pyy = R
Posons +:
x’ = x(v)/h(v)
x' est du point de vue de l'utilité l'équivalent de x(v) en
unités du bien idéal.
En transformant les variables, le problème initial devient:
max U(x’,y)
sous la contrainte :
p(v)h(v)x’ + pyy = R
La première étape de la démarche du consommateur est donc de
déterminer la variété v* rendant minimal p(v)h(v) ; posons px’
= p(v*)h(v*). Ensuite, le consommateur détermine les quantités x’ et y par
max U(x’,y)
sous la contrainte :
px’x’ + pyy = R
Enfin,
x(v*) = x’h(v*).
Au niveau du consommateur, la situation est donc claire : il
n'achètera qu'une variété, v* ; ses préférences entre variétés étant indiquées
par la fonction h(v), il changera ce choix si les prix relatifs des variétés sont
modifiés de telle sorte que le rapport qualité/prix de v* soit moins attractif.
Considérons maintenant l'ensemble des consommateurs. Supposons
qu'ils ont tous la même fonction h(v - v), et que leurs variétés idéales sont
uniformément réparties sur le segment de droite. Le nombre des consommateurs qui
préfèrent la variété v* du point de vue du rapport qualité/prix est alors
proportionnel à la longueur du segment contenant les points tels que p(v - v*)h(v - v*)
soit minimal.
Exemple
Supposons que :
- {v} = [-2, +2],
- il existe deux variétés, d’abscisses -1 et +1,
- h(v) = | v - v|
Dans ce cas, si p(-1) = p(1), le marché se répartit de la
façon suivante :
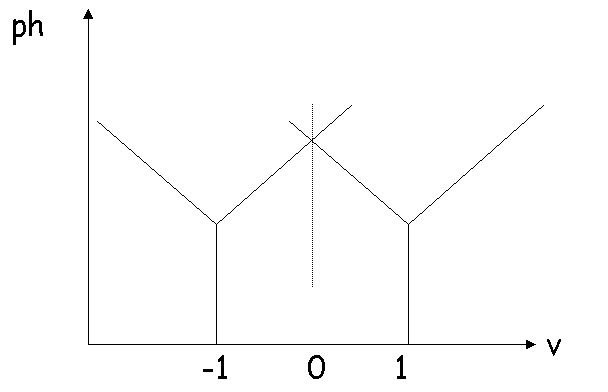
si l’on passe à p(-1) = ½ et p(1) = 1, la répartition
sera :
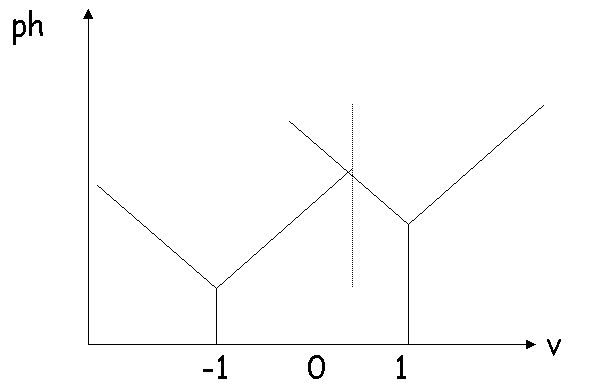
La variété dont le prix relatif s'est élevé a perdu des
clients, mais continue tout de même à se vendre. Lorsque p(1) augmente, cela
entraîne une augmentation du prix que doivent payer les clients qui lui restent fidèles,
donc une baisse de leur consommation de ce produit (puisqu'ils arbitrent entre la
consommation de X et celle de Y en maximisant leur utilité). On a, comme dans le cas du
monopole, une élasticité de la demande au prix. Mais en outre, lorsque p(1) augmente,
certains consommateurs vont décider d'abandonner la variété (1) pour acheter la
variété (-1) : il y a donc entre les monopoles une compétition dont l'enjeu est
l'élargissement de leurs marchés.
Le raisonnement peut se transposer à un autre type de
monopole : celui qui est attaché à la localisation géographique du producteur
lorsque les coûts de transport sont très élevés (produits pondéreux). Le prix d'achat
par un acheteur situé à la distance x du lieu de production est du type p + cx
Parmi les variétés existantes, le consommateur choisira v*
tels que p(v*) + c | v - v*| soit
minimal.
Dans ce cas la fonction de coût à minimiser est additive selon
les prix (et non multiplicative comme lorsque nous considérions des rapports
qualité/prix). Cette approche considère les cas de monopole local. Rien n'interdit, bien
sûr, de combiner les approches " qualité " et " transport " il faut
alors minimiser une fonction du type:
[p(v*) + c | v - v*| ]h(v - v*)
Fonction de demande
Les consommateurs qui se trouvent dans l'intervalle (v, v + dv)
doivent maximiser U(x', y) sous la contrainte :
p(v)h(v)x’ + pyy = R
Cela détermine la quantité x(v) = x'h(v) achetée par le
consommateur type.
Supposons que tous les consommateurs aient le même revenu et
que leur répartition soit uniforme sur [- 2, + 2]. La quantité totale achetée de la
variété 1 est :
Q = (N/4) ò x(v)dv
où N est le nombre total des consommateurs, et la zone
d'intégration la largeur de l'intervalle sur lequel la variété 1 est préférée.
Le prix moyen de la variété 1 est :
ò p(v)x(v)dv
/ ò x(v)dv = D1 / ò x(v)dv
où D1 est la dépense en
produit X des acheteurs de la variété 1.
Considérons le cas où la demande du produit X s'annule
au-delà d'un certain prix (" prix de réservation "). C'est le cas
notamment dans les situations de choix discret : supposons que X soit tel que la
satisfaction dépende seulement de sa possession (x = 1) ou de sa non possession (x = 0)
(exemples: automobile, téléphone, machine à laver etc.) Dans ce cas, le problème du
consommateur devient :
max U(x,y) avec pxx + pyy = R, x = 0 ou x = 1.
Si x = 0, y = R/py
si x = 1, y = (R - px) /py
Le consommateur doit donc comparer les deux niveaux
d’utilité :
U0 = U(0, R/py) et U1 = U[1, (R - px)/py]
Le niveau de R détermine si U0
est supérieur ou inférieur à U1. Pour les ménages
les plus pauvres U0 est plus grand que U1 : quand la consommation du bien durable Y est basse, la
désutilité marginale d’une baisse supplémentaire est grande par rapport au gain
d’utilité procuré par la possession d’un bien durable. Quand R est grand, la
désutilité d’une décroissance en Y est plus que compensée par la possession du
bien durable. Il existe donc un seuil Rs de revenu au
delà duquel le bien X est acheté, au dessous duquel il ne l’est pas.
Si px baisse, la courbe U1 glisse vers le haut (on peut acheter du bien Y en plus grande
quantité) et le seuil Rs diminue.
Le seuil pxs à partir
duquel le produit n’est plus acheté dépend du niveau de revenu du consommateur ;
comme les revenus sont dispersés dans une population concrète, il n’y aurait pas en
principe de disparition brutale de la consommation pour un seuil de prix, mais une
disparition progressive. Cependant, si l’on tient compte du fait que la demande
d’un bien durable ne se déclenche que lorsque le taux d’équipement a franchi
un certain niveau, en raison de l’homogénéité des styles de vie et des effets
d’exemplarité, l’image du seuil précis approche correctement la réalité. On
peut donc supposer sans dommage que tous les consommateurs ont le même revenu.
La courbe de demande prend alors une forme très particulière :
- au dessus de pxs la
demande est nulle,
- pour des valeurs faiblement inférieures à pxs, la zone d’influence du producteur est étroite, et elle
est entourée par une zone dans laquelle les consommateurs n’achètent pas X :
- lorsque p(v) diminue suffisamment, les zones d’influence
des producteurs se touchent,
- si p(v) diminue davantage, la zone d’influence de v
s’étend au détriment de ses voisins : c’est la concurrence !
On est donc en situation de monopole si p(v) est grand, en
situation de concurrence si p(v) diminue.
Pour préciser les choses, supposons que nous avons affaire
l’on considère des frais de transport :
p’ = p + cx,
un producteur pratique le prix p, entouré d’autres
producteurs distribués également sur un cercle et pratiquant tous le prix p, la
distance entre deux producteurs étant 1/n.
Soit ps le prix maximal du
bien X. La zone d’influence du producteur s’étend jusqu’à x tel
que
p + cx £ ps,
d’où
x = (ps - p)/c
Si l’on suppose que la circonférence du cercle est de
longueur unité et que le nombre de consommateurs est L, on trouve la demande de monopole
:
qm = (2L/c)(ps - p)
Si p diminue, le producteur va entrer en concurrence avec ses
voisins. Il est choisi si:
p + cx < p + c [(1/n) - x]
la limite est x tel que : x = (p - p + c/n)/2c
La demande de concurrence est :
qc = (L/c)(p - p +
c/n)
Le seuil de prix où l’on passe du monopole à la
concurrence est :
pl = 2ps - p - c/n
Le seuil de contact en x est :
xl = (p - ps + c/n)/c
ql = (2L/c)(p - ps + c/n)
On remarque que la pente de la courbe qm
est -(c/2L), que la pente de la courbe ql est -(c/L)
; il y a donc un " coin " au point (ql,
pl).
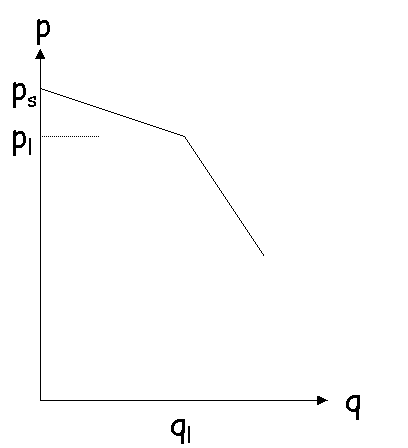
Si p continue à baisser, le producteur va capturer le marché
de ses voisins. Cela se passe brutalement:
Le seuil est atteint lorsque :
x = 1/n
ou autrement dit
p = p - c/n
D'un seul coup, le marché atteint est multiplié par 1,5. Puis
le producteur entre en concurrence avec les producteurs situés au-delà de ses
concurrents les plus proches, etc.
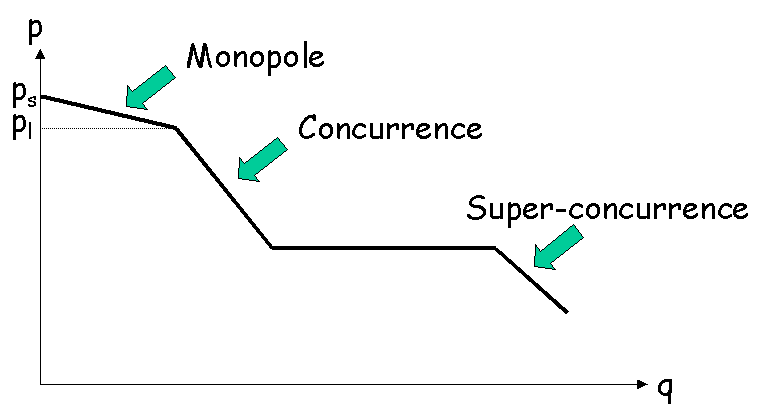
Ce graphique illustre la concurrence en équilibre monopoliste.
La courbe ci-dessus, avec sa forme anguleuse, représente la demande adressée à
l'entreprise produisant une variété, en supposant fixes les qualités et prix des
variétés fournies par les autres entreprises.
Tant que le prix est élevé, le marché se limite aux clients
qui préfèrent cette variété-là et par rapport auxquels l'entreprise a donc un
monopole de fait. Si le prix baisse, le marché s'étend à des clients qui
préféreraient d'autres variétés, mais qui en comparant les rapports qualité/prix
peuvent trouver avantageux d'acheter une variété a priori plus éloignée de
leurs goûts. Si la baisse continue, l'entreprise va à partir d'un certain seuil rafler
d'un coup le marché des variétés voisines, et sera en concurrence avec les variétés
situées un cran plus loin dans le pavage de l'espace des besoins.
Supposons que nous soyons dans une économie à coût fixe et à
forte innovation. Si une entreprise met en œuvre un procédé nouveau diminuant le
coût fixe, elle déterminera son prix de manière à maximiser son chiffre d'affaires en
tenant compte de la courbe de demande ci-dessus. Elle pourra ainsi éventuellement
évincer les fournisseurs voisins.
Annexe 2 du chapitre IV : L’entrepreneur du STC
L’économie du STC sécrète sur le comportement des
entrepreneurs une ambiguïté qui peut lui être mortelle. Ils vivent dans le monde du
risque à l'état pur, puisqu'ils gèrent des fonctions de production à coût fixe. Or
une entreprise vit tant que ses créanciers estiment pouvoir recouvrer leurs créances ;
elle meurt le jour où ils jugent plus sûr de provoquer sa liquidation pour récupérer
une partie de leur créance, car ils ont perdu confiance en sa capacité à rembourser la
totalité.
L’entrepreneur du STC n'a pas d'autre solution, pour faire
survivre son entreprise, que d'afficher une assurance sereine devant les créanciers même
s'il est conscient des incertitudes et si chaque nouveau projet met en péril
l'entreprise, quels que soient ses succès passés.
Prenons le cas d'une grande entreprise, à l'équilibre
précaire, prisonnière d’un réseau de pouvoir à la fois hiérarchique et féodal.
L’entrepreneur est alors contraint à un jeu d'illusionniste impliquant une part de
mensonge, d'abus de confiance. Il sera un " escroc " s'il en reste là. Il sera
un " héros " si, parallèlement à cette politique d'illusions, il engage la
lutte contre l'ordre souterrain de l'entreprise, les réseaux qui prospèrent sur son dos.
Il montera alors prudemment et discrètement les opérations nécessaires pour passer à
une structure organique libérée des réseaux de pouvoir et sortir de l'ornière.
Pour celui qui voit les choses de l'extérieur, comment savoir
à qui l'on a affaire ? La partie défensive de l'action du héros est la même que celle
de l'escroc : il s'agit de susciter la confiance des créanciers en utilisant l'art de la
communication et l'habileté des attachés de presse. La partie constructive de
l’action est secrète et donc invisible, sinon elle serait inefficace. Il est alors
impossible à un autre que lui-même (ou que son confident, s'il en a un) de discerner
s'il est un héros ou un escroc.
Cette situation est courante dans l'industrie du logiciel,
archétype des industries du STC. Fausses annonces pour occuper le terrain, affichage de
délais non tenables, contrats signés avec dès le départ la ferme intention de ne pas
les respecter, manipulation du marché boursier etc.
Tous les entrepreneurs du STC sont des héros ou des escrocs,
mais rien ne permet de discerner entre ces deux hypothèses - pas même le succès, car il
n'existe pas de succès définitif lorsque l'on est contraint de jouer toujours de nouveau
à quitte ou double. Dès lors la facilité, la crainte de la souffrance, le caractère
pénible de la vie du héros (qui s'attache à des valeurs qu'il est seul à connaître),
poussent fatalement l'entrepreneur vers le rôle de l'escroc, sauf s'il a une structure
morale très solide.
Les vertus morales étant peu répandues, l'abus de confiance
risque de se généraliser. L'incertitude, la prise de risque, seront alors gérées au
" bluff ", et non selon la stratégie qui, sans éliminer le risque, le
limiterait statistiquement. L’escroc jouit des avantages du pouvoir tant que celui-ci
lui appartient. Il se classe parmi les " décideurs ", qui constituent en France
un monde à part ; s'il chute, la solidarité de ce monde lui donnera souvent les moyens
de remonter en selle, le préférant à un " outsider " dépourvu des
bonnes manières qui ne s'acquièrent que par un séjour prolongé dans ce milieu.
Surfer sur les apparences, défendre son domaine d'influence,
adhérer à un ou l'autre des réseaux souterrains qui " font
système " et défendent mécaniquement leurs adhérents, cela peut durer le
temps d'une carrière. Après quoi on prend sa retraite et on dépense les économies
accumulées ; on laisse à sa famille un nom et un patrimoine; on aura tenu son rôle sur
cette terre, pourquoi se casser la tête à vouloir " changer le
monde " ?
Mais ici se noue une contradiction. L’économie du STC, en
même temps qu'elle incite les entrepreneurs à se muer en escrocs, oblige les entreprises
à conclure des partenariats. Or qui dit partenariat dit confiance : le contrat ne suffit
pas, il faut l'engagement des personnes. Et comment faire confiance à des gens dont on ne
peut savoir s'ils sont des héros ou des escrocs, sachant que l'homme le plus doué pour
être un escroc, c'est celui qui sait inspirer confiance ?
Cette contradiction risque d'être mortelle pour le STC. Elle
est de nature à inhiber son potentiel d'efficacité, à contrecarrer les apports de
l'automatisation, à ruiner la confiance dans le crédit, puis de proche en proche dans la
monnaie, à susciter des crises financières destructrices de la possibilité de toute
transaction.
Les remèdes existent : un droit adapté, une jurisprudence, des
magistrats expérimentés peuvent aider à régler les contentieux et diffuser le bon
exemple. Pour le moment cependant le magistrat a le plus souvent une conception normative
du droit et il ignore les conditions pratiques de la gestion des entreprises. Il sera donc
comme les autres, ou plus que les autres, enclin à condamner indistinctement le héros et
l'escroc, puisqu'ils lui présentent la même apparence.
Ce sera le cas si a2/4b > c.
Pour l’entreprise, la difficulté provient du caractère
incertain des paramètres a et b de la fonction de demande.
La demande adressée à l’entreprise dépend aussi des
offres futures des concurrents qui jouxtent le territoire (au sens de l'espace des
besoins) sur lequel elle souhaite détenir un monopole.
Supposons que le marché considéré soit en outre le théâtre
d'une innovation intense. Dans ce cas l'anticipation porte non seulement sur la demande et
l'offre des concurrents, mais sur leurs fonctions de coût : s'ils arrivent à trouver un
procédé qui réduit leur coût fixe, ils pourront se placer sur le segment visé par
l’entrepreneur en pratiquant un prix plus bas que les siens et rafler tout ou partie
de son marché.
Les facteurs d'incertitude sont donc nombreux. L'activité de
l'entrepreneur ressemble à un jeu de hasard où se succèdent des coups à quitte ou
double, et où les succès passés n'apportent aucune garantie pour le futur.
Dans une situation aussi dangereuse, il est naturel que
l’entrepreneur s'efforce de limiter les risques en pratiquant une politique de
partenariat. L'entente avec un concurrent stabilise la frontière avec ce concurrent et
permet de conjuguer les forces pour combattre les autres (notamment en associant les
moyens de recherche pour définir les produits et en alliant les forces commerciales).
D'autres partenariats peuvent être formés avec des entreprises apportant au produit des
qualités complémentaires. La pratique des partenariats est endogène à l'économie à
coût fixe. Le jeu de go, avec ses tactiques d'acquisition de territoire et
d'encerclement, illustre bien la logique de cette économie.
Le partage des territoires, les guerres de frontières, les
partenariats, rappellent l'économie de l'époque féodale, lorsque chaque seigneur, grand
propriétaire foncier, contrôlait un territoire autour de son château-fort, entretenait
la guerre sur ses frontières, et passait avec ses voisins ou son suzerain des accords
sanctionnés par des serments d'autant plus solennels qu'ils étaient bientôt violés. Il
est intéressant d'observer, au sein de l'économie la plus moderne, celle du STC, la
résurgence d'un style économique que l'on pouvait croire révolu. Le risque extrême,
associé en cas de réussite à des profits démesurés, suscite des formes de concurrence
violentes. Les entrepreneurs sont tentés de corrompre les acheteurs pour s'assurer des
débouchés, et pour cela il leur faut constituer des " caisses
noires " illégales. L'économie du STC donne donc du travail à l'appareil
judiciaire : les " affaires " lui sont endogènes.
Consommation
Supposons que sur le marché d'un produit le consommateur trouve
plusieurs variétés différentes (choix entre plusieurs types de pâtes dentifrices,
d'automobiles etc.). La réponse intuitive est immédiate : il choisira le produit
présentant le meilleur rapport qualité/prix. Peu importe ici que la mesure de la
qualité soit " objective " ou " subjective ", qu'elle découle de
différences réelles des variétés ou des images créées par la publicité.
Si le prix d’une variété s’élève, elle perd des
clients, mais continue tout de même à se vendre : c'est l'un des
effets de la différenciation. Si le produit était indifférencié, toutes les
entreprises seraient contraintes à vendre au même prix, car seule l'entreprise qui vend
au prix le plus bas pourrait écouler sa production. Mais ici, comme le produit est
différencié en variétés à chacune desquelles correspond un segment distinct du
marché, la hausse du prix d'une variété n'entraîne pas sa disparition complète.
Ce modèle explique les échanges croisés : chaque pays se
spécialise dans la production de certaines variétés, et ses consommateurs se
répartissent entre tous les segments correspondants à l'ensemble des variétés
produites dans le monde.
La différenciation des produits a pour effet d'amortir
l'incidence des mouvements de prix (et de parité) sur les échanges : dans le cas d'un
produit non différencié, et si le coût relatif du transport est bas, les achats se
réorientent d'une manière brutale, l'offreur qui pratique le prix le plus bas sur le
marché mondial raflant toutes les commandes. D'où le caractère instable des marchés
des matières premières, et la difficulté pour un pays producteur de prévoir la demande
et de planifier ses investissements (surtout lorsque les coûts de production dépendent
d'un facteur aléatoire comme le climat). Par contre, dans le cas de produits
différenciés, la hausse du prix entraîne certes une baisse des quantités, mais non
l'éviction totale du producteur du moins jusqu’à une certaine limite.
Annexe 1 du chapitre IV : Consommation d’un bien
diversifié
Supposons que l'ensemble des variétés possibles soit
représentable de façon continue dans un espace à une dimension, par exemple sur un
segment de droite de longueur 1. Si on suppose de plus les variétés 0 et 1 identiques,
on sera conduit à utiliser une représentation circulaire.
Considérons un consommateur dont la variété " idéale
" est v ; soit ½ v - v½
la longueur de l’arc joignant les variétés v et v.
Supposons que pour ce consommateur la satisfaction apportée par
une unité de v soit égale à la satisfaction apportée par h(v - v)
unités de v, la fonction h ayant les propriétés suivantes :
h(0) = 1
h(x) = h(-x)
h(x) > 1 pour x ¹ 0
dh/| dv|
> 0
d2h/dv2 ³ 0

Supposons que v = 0 pour simplifier les notations. Soit
p(v) le prix de la variété v. Le rapport qualité/prix associé à v est
Q(v) = 1/h(v)p(v)
Le consommateur choisit parmi les variétés offertes sur le
marché celle qui minimise h(v)p(v) (cette quantité représente le prix à payer, si l'on
choisit v, pour obtenir une satisfaction égale à celle que procure une unité de v).
Considérons un consommateur qui utilise deux produits : X, bien
différencié, et Y non différencié. Le problème de ce consommateur est de
maximiser :
U(x,y) = U [x(v)/h(v), y]
sous la contrainte :
p(v)x(v) + pyy = R
Posons +:
x’ = x(v)/h(v)
x' est du point de vue de l'utilité l'équivalent de x(v) en
unités du bien idéal.
En transformant les variables, le problème initial devient:
max U(x’,y)
sous la contrainte :
p(v)h(v)x’ + pyy = R
La première étape de la démarche du consommateur est donc de
déterminer la variété v* rendant minimal p(v)h(v) ; posons px’
= p(v*)h(v*). Ensuite, le consommateur détermine les quantités x’ et y par
max U(x’,y)
sous la contrainte :
px’x’ + pyy = R
Enfin,
x(v*) = x’h(v*).
Au niveau du consommateur, la situation est donc claire : il
n'achètera qu'une variété, v* ; ses préférences entre variétés étant indiquées
par la fonction h(v), il changera ce choix si les prix relatifs des variétés sont
modifiés de telle sorte que le rapport qualité/prix de v* soit moins attractif.
Considérons maintenant l'ensemble des consommateurs. Supposons
qu'ils ont tous la même fonction h(v - v), et que leurs variétés idéales sont
uniformément réparties sur le segment de droite. Le nombre des consommateurs qui
préfèrent la variété v* du point de vue du rapport qualité/prix est alors
proportionnel à la longueur du segment contenant les points tels que p(v - v*)h(v - v*)
soit minimal.
Exemple
Supposons que :
- {v} = [-2, +2],
- il existe deux variétés, d’abscisses -1 et +1,
- h(v) = | v - v|
Dans ce cas, si p(-1) = p(1), le marché se répartit de la
façon suivante :

si l’on passe à p(-1) = ½ et p(1) = 1, la répartition
sera :

La variété dont le prix relatif s'est élevé a perdu des
clients, mais continue tout de même à se vendre. Lorsque p(1) augmente, cela
entraîne une augmentation du prix que doivent payer les clients qui lui restent fidèles,
donc une baisse de leur consommation de ce produit (puisqu'ils arbitrent entre la
consommation de X et celle de Y en maximisant leur utilité). On a, comme dans le cas du
monopole, une élasticité de la demande au prix. Mais en outre, lorsque p(1) augmente,
certains consommateurs vont décider d'abandonner la variété (1) pour acheter la
variété (-1) : il y a donc entre les monopoles une compétition dont l'enjeu est
l'élargissement de leurs marchés.
Le raisonnement peut se transposer à un autre type de
monopole : celui qui est attaché à la localisation géographique du producteur
lorsque les coûts de transport sont très élevés (produits pondéreux). Le prix d'achat
par un acheteur situé à la distance x du lieu de production est du type p + cx
Parmi les variétés existantes, le consommateur choisira v*
tels que p(v*) + c | v - v*| soit
minimal.
Dans ce cas la fonction de coût à minimiser est additive selon
les prix (et non multiplicative comme lorsque nous considérions des rapports
qualité/prix). Cette approche considère les cas de monopole local. Rien n'interdit, bien
sûr, de combiner les approches " qualité " et " transport " il faut
alors minimiser une fonction du type:
[p(v*) + c | v - v*| ]h(v - v*)
Fonction de demande
Les consommateurs qui se trouvent dans l'intervalle (v, v + dv)
doivent maximiser U(x', y) sous la contrainte :
p(v)h(v)x’ + pyy = R
Cela détermine la quantité x(v) = x'h(v) achetée par le
consommateur type.
Supposons que tous les consommateurs aient le même revenu et
que leur répartition soit uniforme sur [- 2, + 2]. La quantité totale achetée de la
variété 1 est :
Q = (N/4) ò x(v)dv
où N est le nombre total des consommateurs, et la zone
d'intégration la largeur de l'intervalle sur lequel la variété 1 est préférée.
Le prix moyen de la variété 1 est :
ò p(v)x(v)dv
/ ò x(v)dv = D1 / ò x(v)dv
où D1 est la dépense en
produit X des acheteurs de la variété 1.
Considérons le cas où la demande du produit X s'annule
au-delà d'un certain prix (" prix de réservation "). C'est le cas
notamment dans les situations de choix discret : supposons que X soit tel que la
satisfaction dépende seulement de sa possession (x = 1) ou de sa non possession (x = 0)
(exemples: automobile, téléphone, machine à laver etc.) Dans ce cas, le problème du
consommateur devient :
max U(x,y) avec pxx + pyy = R, x = 0 ou x = 1.
Si x = 0, y = R/py
si x = 1, y = (R - px) /py
Le consommateur doit donc comparer les deux niveaux
d’utilité :
U0 = U(0, R/py) et U1 = U[1, (R - px)/py]
Le niveau de R détermine si U0
est supérieur ou inférieur à U1. Pour les ménages
les plus pauvres U0 est plus grand que U1 : quand la consommation du bien durable Y est basse, la
désutilité marginale d’une baisse supplémentaire est grande par rapport au gain
d’utilité procuré par la possession d’un bien durable. Quand R est grand, la
désutilité d’une décroissance en Y est plus que compensée par la possession du
bien durable. Il existe donc un seuil Rs de revenu au
delà duquel le bien X est acheté, au dessous duquel il ne l’est pas.
Si px baisse, la courbe U1 glisse vers le haut (on peut acheter du bien Y en plus grande
quantité) et le seuil Rs diminue.
Le seuil pxs à partir
duquel le produit n’est plus acheté dépend du niveau de revenu du consommateur ;
comme les revenus sont dispersés dans une population concrète, il n’y aurait pas en
principe de disparition brutale de la consommation pour un seuil de prix, mais une
disparition progressive. Cependant, si l’on tient compte du fait que la demande
d’un bien durable ne se déclenche que lorsque le taux d’équipement a franchi
un certain niveau, en raison de l’homogénéité des styles de vie et des effets
d’exemplarité, l’image du seuil précis approche correctement la réalité. On
peut donc supposer sans dommage que tous les consommateurs ont le même revenu.
La courbe de demande prend alors une forme très particulière :
- au dessus de pxs la
demande est nulle,
- pour des valeurs faiblement inférieures à pxs, la zone d’influence du producteur est étroite, et elle
est entourée par une zone dans laquelle les consommateurs n’achètent pas X :
- lorsque p(v) diminue suffisamment, les zones d’influence
des producteurs se touchent,
- si p(v) diminue davantage, la zone d’influence de v
s’étend au détriment de ses voisins : c’est la concurrence !
On est donc en situation de monopole si p(v) est grand, en
situation de concurrence si p(v) diminue.
Pour préciser les choses, supposons que nous avons affaire
l’on considère des frais de transport :
p’ = p + cx,
un producteur pratique le prix p, entouré d’autres
producteurs distribués également sur un cercle et pratiquant tous le prix p, la
distance entre deux producteurs étant 1/n.
Soit ps le prix maximal du
bien X. La zone d’influence du producteur s’étend jusqu’à x tel
que
p + cx £ ps,
d’où
x = (ps - p)/c
Si l’on suppose que la circonférence du cercle est de
longueur unité et que le nombre de consommateurs est L, on trouve la demande de monopole
:
qm = (2L/c)(ps - p)
Si p diminue, le producteur va entrer en concurrence avec ses
voisins. Il est choisi si:
p + cx < p + c [(1/n) - x]
la limite est x tel que : x = (p - p + c/n)/2c
La demande de concurrence est :
qc = (L/c)(p - p +
c/n)
Le seuil de prix où l’on passe du monopole à la
concurrence est :
pl = 2ps - p - c/n
Le seuil de contact en x est :
xl = (p - ps + c/n)/c
ql = (2L/c)(p - ps + c/n)
On remarque que la pente de la courbe qm
est -(c/2L), que la pente de la courbe ql est -(c/L)
; il y a donc un " coin " au point (ql,
pl).

Si p continue à baisser, le producteur va capturer le marché
de ses voisins. Cela se passe brutalement:
Le seuil est atteint lorsque :
x = 1/n
ou autrement dit
p = p - c/n
D'un seul coup, le marché atteint est multiplié par 1,5. Puis
le producteur entre en concurrence avec les producteurs situés au-delà de ses
concurrents les plus proches, etc.

Ce graphique illustre la concurrence en équilibre monopoliste.
La courbe ci-dessus, avec sa forme anguleuse, représente la demande adressée à
l'entreprise produisant une variété, en supposant fixes les qualités et prix des
variétés fournies par les autres entreprises.
Tant que le prix est élevé, le marché se limite aux clients
qui préfèrent cette variété-là et par rapport auxquels l'entreprise a donc un
monopole de fait. Si le prix baisse, le marché s'étend à des clients qui
préféreraient d'autres variétés, mais qui en comparant les rapports qualité/prix
peuvent trouver avantageux d'acheter une variété a priori plus éloignée de
leurs goûts. Si la baisse continue, l'entreprise va à partir d'un certain seuil rafler
d'un coup le marché des variétés voisines, et sera en concurrence avec les variétés
situées un cran plus loin dans le pavage de l'espace des besoins.
Supposons que nous soyons dans une économie à coût fixe et à
forte innovation. Si une entreprise met en œuvre un procédé nouveau diminuant le
coût fixe, elle déterminera son prix de manière à maximiser son chiffre d'affaires en
tenant compte de la courbe de demande ci-dessus. Elle pourra ainsi éventuellement
évincer les fournisseurs voisins.
Annexe 2 du chapitre IV : L’entrepreneur du STC
L’économie du STC sécrète sur le comportement des
entrepreneurs une ambiguïté qui peut lui être mortelle. Ils vivent dans le monde du
risque à l'état pur, puisqu'ils gèrent des fonctions de production à coût fixe. Or
une entreprise vit tant que ses créanciers estiment pouvoir recouvrer leurs créances ;
elle meurt le jour où ils jugent plus sûr de provoquer sa liquidation pour récupérer
une partie de leur créance, car ils ont perdu confiance en sa capacité à rembourser la
totalité.
L’entrepreneur du STC n'a pas d'autre solution, pour faire
survivre son entreprise, que d'afficher une assurance sereine devant les créanciers même
s'il est conscient des incertitudes et si chaque nouveau projet met en péril
l'entreprise, quels que soient ses succès passés.
Prenons le cas d'une grande entreprise, à l'équilibre
précaire, prisonnière d’un réseau de pouvoir à la fois hiérarchique et féodal.
L’entrepreneur est alors contraint à un jeu d'illusionniste impliquant une part de
mensonge, d'abus de confiance. Il sera un " escroc " s'il en reste là. Il sera
un " héros " si, parallèlement à cette politique d'illusions, il engage la
lutte contre l'ordre souterrain de l'entreprise, les réseaux qui prospèrent sur son dos.
Il montera alors prudemment et discrètement les opérations nécessaires pour passer à
une structure organique libérée des réseaux de pouvoir et sortir de l'ornière.
Pour celui qui voit les choses de l'extérieur, comment savoir
à qui l'on a affaire ? La partie défensive de l'action du héros est la même que celle
de l'escroc : il s'agit de susciter la confiance des créanciers en utilisant l'art de la
communication et l'habileté des attachés de presse. La partie constructive de
l’action est secrète et donc invisible, sinon elle serait inefficace. Il est alors
impossible à un autre que lui-même (ou que son confident, s'il en a un) de discerner
s'il est un héros ou un escroc.
Cette situation est courante dans l'industrie du logiciel,
archétype des industries du STC. Fausses annonces pour occuper le terrain, affichage de
délais non tenables, contrats signés avec dès le départ la ferme intention de ne pas
les respecter, manipulation du marché boursier etc.
Tous les entrepreneurs du STC sont des héros ou des escrocs,
mais rien ne permet de discerner entre ces deux hypothèses - pas même le succès, car il
n'existe pas de succès définitif lorsque l'on est contraint de jouer toujours de nouveau
à quitte ou double. Dès lors la facilité, la crainte de la souffrance, le caractère
pénible de la vie du héros (qui s'attache à des valeurs qu'il est seul à connaître),
poussent fatalement l'entrepreneur vers le rôle de l'escroc, sauf s'il a une structure
morale très solide.
Les vertus morales étant peu répandues, l'abus de confiance
risque de se généraliser. L'incertitude, la prise de risque, seront alors gérées au
" bluff ", et non selon la stratégie qui, sans éliminer le risque, le
limiterait statistiquement. L’escroc jouit des avantages du pouvoir tant que celui-ci
lui appartient. Il se classe parmi les " décideurs ", qui constituent en France
un monde à part ; s'il chute, la solidarité de ce monde lui donnera souvent les moyens
de remonter en selle, le préférant à un " outsider " dépourvu des
bonnes manières qui ne s'acquièrent que par un séjour prolongé dans ce milieu.
Surfer sur les apparences, défendre son domaine d'influence,
adhérer à un ou l'autre des réseaux souterrains qui " font
système " et défendent mécaniquement leurs adhérents, cela peut durer le
temps d'une carrière. Après quoi on prend sa retraite et on dépense les économies
accumulées ; on laisse à sa famille un nom et un patrimoine; on aura tenu son rôle sur
cette terre, pourquoi se casser la tête à vouloir " changer le
monde " ?
Mais ici se noue une contradiction. L’économie du STC, en
même temps qu'elle incite les entrepreneurs à se muer en escrocs, oblige les entreprises
à conclure des partenariats. Or qui dit partenariat dit confiance : le contrat ne suffit
pas, il faut l'engagement des personnes. Et comment faire confiance à des gens dont on ne
peut savoir s'ils sont des héros ou des escrocs, sachant que l'homme le plus doué pour
être un escroc, c'est celui qui sait inspirer confiance ?
Cette contradiction risque d'être mortelle pour le STC. Elle
est de nature à inhiber son potentiel d'efficacité, à contrecarrer les apports de
l'automatisation, à ruiner la confiance dans le crédit, puis de proche en proche dans la
monnaie, à susciter des crises financières destructrices de la possibilité de toute
transaction.
Les remèdes existent : un droit adapté, une jurisprudence, des
magistrats expérimentés peuvent aider à régler les contentieux et diffuser le bon
exemple. Pour le moment cependant le magistrat a le plus souvent une conception normative
du droit et il ignore les conditions pratiques de la gestion des entreprises. Il sera donc
comme les autres, ou plus que les autres, enclin à condamner indistinctement le héros et
l'escroc, puisqu'ils lui présentent la même apparence.
|