Chapitre II : Rendements croissants

(extrait de Michel Volle, e-conomie, Economica 2000)

Fonction de production et fonction de coût

La « fonction de production » d’une entreprise donne la quantité produite Y en fonction des volumes de facteurs de production consommés : capital (K) et travail (L) :

(1) Y = f(K, L).

C’est une relation entre quantités physiques, les prix n’y interviennent pas. K mesure le volume du capital physique utilisé dans la production : on peut l’interpréter comme un « nombre de machines ». Le travail L est la quantité de travail consommée dans un intervalle de temps : ce sera par exemple le nombre d’heures de travail consommées en une année. K est une variable de stock, L une variable de flux.

On dit que la fonction de production est à rendement constant (on encore « homogène de degré un ») si, lorsqu’on multiplie les quantités des facteurs par un coefficient la production est multipliée par le même coefficient :

(2) f(λK, λL) = λf(K, L)

Lorsque λ>1, le rendement est croissant si f(λK, λL) > λf(K, L), décroissant si f(λK, λL) < λf(K, L). Une même fonction de production peut être à rendement croissant sur certaines plages de valeurs de K et de L, à rendement décroissant sur d’autres plages de valeurs.

Les économistes utilisent diverses spécifications de la fonction de production entre lesquelles ils choisissent selon le problème à traiter :

-         fonction de Cobb-Douglas :
Y = aK^αL^β , avec a, α et β > 0.
Le rendement est :
constant si α + β = 1,
croissant si α + β > 1,
décroissant si α + β < 1.  

-         fonction à élasticité de substitution constante (CES)[1] :
Y = a[(1 - α)K^{(σ -1)/ σ} + α L^{(σ -1)/ σ} ] ^{σ /( σ - 1)},

-         fonction à facteurs complémentaires :
Y = min (aK^α ; bL^β).

Si l’on connaît les prix unitaires[2] r et w des facteurs K et L, on peut déterminer la combinaison des facteurs K et L permettant de produire la quantité Y pour un coût minimal. On appelle « fonction de coût » l’expression c(Y) qui associe à Y son coût minimal de production (cf. annexe du chapitre).

Lorsque l’on connaît la fonction de coût, on peut définir les rendements en termes de coût. Les expressions « rendement croissant » ou « rendement décroissant » s’appliquent alors, selon le contexte, soit au coût moyen de production, soit au coût marginal.

Une des formes les plus classiques de la fonction de coût est celle où la concavité de la courbe représentative est dirigée d’abord vers le bas, puis vers le haut :

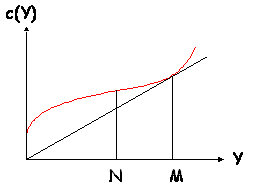
Si l’on considère le coût moyen c(Y) = c(Y)/Y, on dira que le rendement est croissant si c(Y) diminue lorsque la production augmente, qu’il est décroissant dans le cas contraire. Dans le cas représenté par le graphique ci-dessus, le rendement est croissant pour Y < M, et décroissant pour Y > M.

Si l’on considère le coût marginal c’(Y) = dc/dY, on dira que le rendement est croissant si c’’(Y) < 0, qu’il est décroissant si c’’(Y) > 0. Notons N l’abscisse du point d’inflexion dans le graphique ci-dessus. Le rendement défini par référence au coût marginal est croissant pour Y < N, et décroissant pour Y > N.

Les deux notions sont donc compatibles, sauf si Y est compris entre N et M : dans le cas où le rendement est d’abord croissant, puis décroissant, le changement de signe du rendement se produit plus tôt si l’on considère le coût marginal que si l’on considère le coût moyen.

Considérons une fonction de production « à coût fixe » : c(Y) est alors une constante indépendante de la quantité produite. Dans ce cas, c’(Y) = c’’(Y) = 0 : l’examen du coût marginal ne donne aucune information sur le rendement ; par contre, le coût moyen diminue indéfiniment lorsque Y croît. On est donc en rendement croissant.

En supposant les fonctions de production « à coût fixe » et donc le coût marginal nul, nous sommes dans un cas extrême de rendement croissant : pour que le coût moyen décroisse davantage lorsque le volume de la production croît, il faudrait que le coût total décrût, hypothèse qui n’est jamais vérifiée en pratique.

Notons c le coût fixe, supposons que le prix de vente soit p, posons Q = c/p. Si la quantité demandée pour le prix p est supérieure à Q, l’entreprise fait un profit ; si elle est inférieure à Q, l’entreprise fait une perte. La confrontation entre le coût fixe et l’anticipation de demande détermine la décision d’investissement.

L’hypothèse des rendements décroissants

Les formulations les plus simples et les plus puissantes de la théo­rie économique postulent que les fonctions de production sont à rendements décroissants[3] ; lorsqu’elles admettent que la fonction de coût comporte une zone initiale à rendement croissant, elles supposent la demande suffisamment forte pour que l’équilibre économique conduise à produire dans la zone des rendements décroissants.

Cette hypothèse, dite « néoclassique », procure des résultats mathématiques puissants fondés sur la convexité de la zone de production ; elle fonde l'équilibre de concurrence par­faite, permet de construire des courbes d'offre (prix égal au coût margi­nal), de raisonner en équilibre partiel, etc. Elle est à la base de l’enseignement de la théorie économique. John Hicks a cru que son aban­don « ruinerait la plus grande part de la théorie économique[4] ».

Outre leurs vertus théoriques, les rendements décroissants existent bien sûr dans les faits : par exemple en agriculture les parcelles sont ensemencées dans l'ordre des fertilités décroissantes. Sont‑ils pour autant universels ? Il est prudent de répondre à cette question par la négative, car il peut exister des secteurs où la zone des rendements croissants s’étend jusqu’à des niveaux de production permettant de satisfaire toute la demande ; depuis les débuts de la science économique certains économistes ont donc exploré l'hypothèse des rendements croissants. Cette réflexion, longtemps minoritaire, n'a jamais cessé.

Dans les dernières décennies l'intérêt pour les rendements croissants s'est accru ; leur théorie s'est enrichie et ses difficultés ont été prises d'assaut. La question est d'actualité : les rendements croissants sont au cœur du procès intenté à Microsoft par le gouvernement des États‑Unis. Les camps se forment, la polémique fait rage.

Origines de l’hypothèse des rendements croissants

Adam Smith explique la spécialisation et la croissance économiques par les rendements croissants que procure la division du travail[5] et leur assigne pour seule limite la dimension du marché. Mais ce point de vue fut abandonné par Ricardo et Stuart Mill, qui avaient besoin de rendements constants pour définir l'équilibre concurrentiel et lier la valeur aux coûts de production. A partir de ces auteurs, c’est l’hypothèse des rendements décroissants qui est retenue par la majorité des économistes.

Cournot[6] développa pourtant les théories du monopole et de l'oligopole pour traiter les situations de rendement croissant, et Marshall[7] lui-même les a évoquées pour fonder la théorie des externalités. Puis quelques économistes continuent à creuser le sujet : dans les années 30, Edward Chamberlin[8] et Joan Robinson[9] construisirent des modèles de concurrence monopoliste, c'est‑à‑dire de concurrence avec rendements croissants. Nicholas Kaldor a étudié dans les années 1950 leurs effets sur la croissance économique.

L’intérêt pour cette voie de recherche renaît à la fin des années 70 : des économistes américains ‑ Mike Spence, Avinash Dixit, Joe Stiglitz, Kelvin Lancaster, Steve Salop, Paul Krugman ‑ l’utilisent essentiellement pour perfectionner la théorie des échanges internationaux : il s'agit d'expliquer les échanges croisés (« comment se fait‑il que simultanément la France vende des automobiles à l'Allemagne, et l'Allemagne vende des automobiles à la France ? ») et la localisation des industries[10]. Leurs travaux sont relayés en France par un théoricien de la concurrence imparfaite comme Jean Tirole[11].

Brian Arthur commence en 1979 ses recherches sur les processus stochastiques présidant à la sélection de l'équilibre en rendements croissants[12] et sur l'enfermement (« lock‑in ») éventuel d'une économie dans un équilibre inefficace en cas de choix irréversible (« path dependance »)[13].

En 1981 Elhanan Helpman[14] articule les théories classiques du commerce international avec les rendements croissants. Mike Spence[15] étudie les relations entre les rendements croissants et les nouvelles technologies.

Au début des années 80, les travaux sur le commerce international et les rendements croissants reçoivent le nom de « nouvelle théorie du commerce ». Helpman et Krugman en publient la synthèse[16]. L'étude de Paul Romer[17] sur les rendements croissants, la croissance économique et le « progrès technique endogène[18] » devient le point de départ d’une « nouvelle théorie de la croissance »[19].

Apport des rendements croissants

Les rendements croissants sont dès lors un des thèmes importants de la réflexion économique. Si l’on suppose la fonction de production à coût fixe, le rendement est croissant quel que soit le volume de la production ; alors le marché du bien considéré obéit soit au régime de monopole ou d’oligopole, soit au régime de concurrence monopoliste, mais en aucun cas au régime de concurrence parfaite.

Certains économistes, attachés à la limpidité du modèle néoclassique, peut‑être aussi vic­times du conformisme optimiste que ce modèle suscite parfois[20], croient devoir continuer à douter de l’existence des rendements croissants. Il n’est pas facile en effet, lorsque l’on s’est habitué au modèle néoclassique, d’accepter le modèle de concurrence monopoliste qui semble a priori plus compliqué et donc sans doute moins fécond au plan théorique en termes de rapport entre portée des résultats et complexité des hypothèse. Mais d'autres, comme Arrow qui a amplement prouvé sa maîtrise du modèle néoclassique, mani­festent un vif intérêt pour ces développements.

Certaines des questions soulevées par la théorie des rendements croissants sont d’ailleurs moins nouvelles qu'on ne le dit. Ainsi, la multiplicité des équilibres existe dans le modèle néoclassique, et il n'est donc pas besoin des rendements croissants pour l'introduire[21]. Par ailleurs, les décisions des agents économiques sont souvent prises sur la base d'anticipations erronées ou hasardeuses, et ils ne peuvent pas refaire l'histoire lorsque les conséquences de leurs choix se révèlent négatives : on peut donc expliquer la « path dependance » avec la théorie des anticipations, sans faire appel aux rendements croissants. Les exemples souvent évoqués pour illustrer le « lock‑in » peuvent être discutés indéfiniment (choix du clavier QWERTY, des systèmes d'exploitation MS‑DOS et Windows, de la norme VHS[22]).

On peut dire toutefois qu’avec les rendements croissants le risque d'erreur est plus élevé : comme tout le coût de production est payé dès le début, la part du pari sur le futur est plus forte ; en outre, en situation de monopole, la concentration de la décision diminue les chances de correction d’un choix erroné. Donc si les rendements croissants n'expliquent pas seuls le « lock‑in » ils en accroissent la probabilité.

L'apport le plus intéressant des récents travaux sur les rendements croissants nous semble résider dans l'élucidation des formes nouvelles de concurrence ou, plus précisément, d’un nouveau « style » économique. Reprenons un développement de Brian Arthur[23] :

Il s'agit de tenir l'adversaire à distance du marché que l'on convoite. La tactique utilise les fausses annonces, les alliances souvent renouvelées et rompues. Le stratège doit maîtriser des effets de « feedback » négatifs ou positifs qui s'entrelacent en un contrepoint complexe, chacun selon son propre rythme. Ce tableau évoque l'art de la guerre de Sunzi[24], qui est essentiellement l'art de déconcerter l'adversaire.

Les polémiques récentes

Ces nouvelles formes de concurrence suscitent un débat où les rendements croissants et les phénomènes qui leur sont attachés sont souvent évoqués. « Wired », la revue des « branchés » américains, appelle Gates « the Lord of Lock‑in », car nombreux sont ceux qui pensent que Microsoft a enfermé les PC dans un système d'exploitation sous-optimal. Les défenseurs de Microsoft nient que l'on puisse prouver les effets négatifs du « lock‑in », et affirment que les utilisateurs bénéficient de la baisse des prix que permettent les rendements croissants.

La polémique s'est envenimée au début de 1998. Paul Krugman, dans un article de « Slate », revue électronique de Microsoft, a reproché à Brian Arthur de s'attribuer le mérite de la théorie des rendements croissants[25]. Arthur a vu dans cet article la riposte de Microsoft à son intervention dans une conférence de Ralph Nader[26] . Arrow a écrit à Slate pour soutenir Arthur... Ces passes d'armes rappellent les expertises économiques contradictoires publiées, avant le démembrement d'AT&T, à propos du monopole naturel dans les télécommunications.

L’enjeu de ces controverses n'est sans doute pas de savoir s'il existe ou non des rendements croissants, si le lock‑in a des effets négatifs, encore moins d'établir une antériorité entre chercheurs : il réside dans les nouvelles formes de concurrence et de stratégie d'entreprise corrélatives des rendements croissants, et dont Bill Gates est l'acteur le plus visible[27].

Le procès intenté à Microsoft vise en première analyse à contenir un monopole de fait des systèmes d'exploitation, progiciels et applications pour PC. Plus profondément, il faut y voir une réaction contre le jeu économique inédit que suscitent les rendements croissants, jeu devant lequel le droit, l'expertise, les habitudes sont également déconcertés. Or pour maîtriser un tel jeu il ne sert à rien de réagir contre : il faut d'abord le comprendre.

Annexe 1 : Fonction de production et fonction de coût

 Définition de la fonction de coût

Considérons une entreprise dont la fonction de production est :

(1) Y = f(K, L)

Notons p le prix de Y, w le salaire horaire, r la rémunération « normale » de l’utilisation d’une machine pendant un an, p_K le prix d’achat d’une machine.  Supposons w et r exogènes.

La minimisation du coût de production pour produire la quantité Y si w et r sont donnés implique des quantités K et L des facteurs telles que :

(2) w (=) λ∂Y/∂L,

(3) r (=)λ∂Y/∂K.

(Nous utilisons le signe (=) pour noter les égalités vérifiées à l’équilibre ; elles se distinguent des égalités comme (1) qui représentent des définitions).

Notons c(Y) le coût de production de Y. La fonction c(Y) est la « fonction de coût » de l’entreprise. λ est égal au coût marginal c’(Y)[28].

Si en outre l’entreprise maximise son profit :

- en concurrence parfaite, le prix p est exogène et Y doit être tel que :

(4) Y (=) c’^-1(p) 

- en situation de monopole (ou de concurrence monopoliste), la demande p(Y) est exogène et Y doit être tel que :

(5) c’(Y) (=) Yp’(Y) + p(Y) ; c’(Y) est inférieur à p(Y), car p’(Y) est négatif. Donc :

(6) p (=) µc’(Y), où µ > 1 est le « taux de marge » par rapport au coût marginal.

Si en outre le marché est à l’équilibre concurrentiel avec libre entrée (ce qui ne peut se produire qu’en situation de concurrence parfaite ou de concurrence monopoliste, mais non en situation de monopole) :

 (7) pY (=) wL + rK

L’« annulation du profit » que symbolise cette équation ne signifie pas que l’entreprise ne fasse pas de profit comptable, ni qu’elle ne distribue pas de dividendes : le profit qu’elle dégage permet de rémunérer les actionnaires au niveau d’équilibre compte tenu du risque qu’ils ont pris. Il vaut mieux parler de « norme de profit » que de profit nul.

Le « taux de rentabilité interne » (TRI) de l’entreprise est le taux d’actualisation qui annule sa « valeur actuelle nette » (VAN) ; dans le cas considéré ici, la VAN correspondant au taux d’actualisation T est :

(8) VAN = - p_KK + (pY - wL) / T, d’où :

(9) TRI (=) (pY - wL) / p_KK (=) r / p_K = i + π,

où i est le taux d’intérêt sans risque et π la « prime de risque » d’équilibre, c’est-à-dire la prime qui rémunère « normalement » le risque pris par l’actionnaire ; selon la théorie du risque :

(10) π (=) β(τ_M – i), avec :

(11) β = cov(X, M)/σ²_M

où τ_M est le taux de rentabilité interne du marché, σ _X et σ _M les écarts types respectifs des rendements de l’entreprise X et du marché, cov(X, M) leur covariance.

Le prix d’utilisation r du capital est ainsi :

(12) r (=) (i + π)p_K

r n’est donc pas comme on le dit parfois égal au taux d’intérêt du marché i. Si tout le capital avait été emprunté (ou si les actionnaires s’étaient endettés pour le financer), il faudrait ip_KK pour payer les intérêts de l’emprunt ; la rémunération nette du capital est donc égale à πp_KK, et dépend de la prime de risque. L’équation (12) est compatible avec une rémunération « normale » des actionnaires (que ce soit sous forme de dividendes ou d’une plus value correspondant à l’accroissement du capital par autofinancement). La capitalisation boursière de l’entreprise est alors égale à la valeur p_KK de son capital, c’est-à-dire à son actif net[29].

Calcul de la fonction de coût

A titre d’exemple, calculons les fonctions de coût associées aux fonctions de production classiques. Il s’agit de choisir la combinaison (K, L) qui minimise le coût de production d’une quantité Y donnée, w et r étant exogènes et donnés. Cela conduit à identifier la fonction de coût c(Y) qui pour chaque quantité indique le coût de production minimal.

Fonction de Cobb-Douglas

Considérons l’isoquante correspondant à la quantité Y : K et L sont tels que :

(13)Y = aK^αL^β                                              

Cherchons sur cette isoquante le couple (K, L) qui minimise le coût. En ce point, il existe λ tel que :

(14) ∂Y/∂K = aαK ^α-1L^β = λr             

(15) ∂Y/∂L = aβK^αL^β-1 = λw              

L ’élimination de λ entre (14) et (15) donne :

(16) aαK^α-1L^{β }= aβK^αL^β-1r/w

d ’où

(17) K/L = (w/r)(α/β)

Remplaçons K dans (13) par son expression en fonction de L ; cela donne L en fonction de Y :

(18) L = (Y/a)^{1/(α + β)}[(w/r)(α/β)]^{- α /(α + β)}, et par symétrie :

(19) K = (Y/a) ^{1/(α + β)} [(r/w)(β/α)]^{- β /(α + β)},

d ’où le coût de production de Y :

(20) c(Y) = wL + rK

(21) c(Y) = [Yw ^βr ^α(α/β) ^β/a]^/(α+β) (α+β)/α

Cette expression montre l’incidence, sur le coût de production, des divers paramètres α, β, w et r. Il est intéressant d’observer la forme que prend, lorsque ces paramètres sont fixés, la relation entre c(Y) et Y :

(22) c(Y) = γY^1/(α+β), γ étant une constante regroupant tous les termes autres que la puissance de Y.

Si α + β > 1, le rendement en termes de coût est croissant puisque c(Y) est de la forme γY^δ, et que :

(23) δ = 1/(α + β) < 1 (le coût de production croît moins vite que la quantité produite).

Si α + β < 1, le rendement est décroissant.

Fonction à facteurs complémentaires

(24) Y = min (aK ^α ; bL ^β), avec a, b, α, β > 0

Cette fonction rend compte des cas où les quantités de facteurs à utiliser dépendent l’une de l’autre. Ici, on trouve :

(25) L = (a/b)^{1/ β} K^α/β

et réciproquement :

(26) K = (b/a)^{1/ α} L^β/α

Le capital est donc une fonction puissance du travail d’exposant β/α.

Pour produire Y, il faut au moins (Y/a)^1/α de K et (Y/b)^1/β de L, d’où la fonction de coût en supposant les coûts unitaires r et w exogènes :

(27) c(Y) = r(Y/a)^1/α + w(Y/b)^1/β

Si β < 1 < α  ou α < 1 < β le rendement est tantôt croissant, tantôt décroissant. Par exemple avec la fonction de production :

(28) Y = min (K⁵ ; 5L^0,2) et w = r = 1,

le coût moyen est minimal pour Y* = 3,82 et la fonction de coût a l’allure suivante :

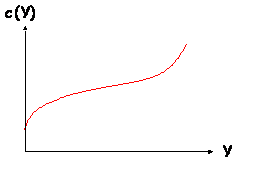
Le cas où les valeurs de α et β entourent 1 donne à la fonction de production une forme souvent rencontrée en pratique, celle où les rendements sont d’abord croissants, puis décroissants. Il permet aussi de construire un équilibre de concurrence parfaite avec une taille d’entreprise non nulle, ce qui n’est pas le cas si les rendements sont continûment décroissants (dans ce cas en effet il faut que le nombre et la taille des entreprises soient exogènes, car sinon on trouvera que les entreprises ont toutes la taille minimale et emploient un seul salarié).

On obtient une fonction à coût fixe à partir de (4) en prenant β petit et α et b grands :  tout se passe alors comme si le coût du travail était (pratiquement) nul tant que Y < b, et devenait très grand lorsque Y atteint ou dépasse b. Si l’on prend une petite valeur pour b, on obtient une fonction de coût que nous retrouverons au chapitre VIII lorsque nous étudierons le coût des réseaux.

Si l’on considère par exemple la fonction de production suivante :

(29) Y = min (K¹⁰⁰ ; 5L^0,001) et w = r = 1,

le graphe de la fonction de coût est :

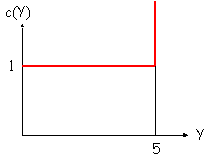
Annexe 2 : valorisation des entreprises

Le texte ci-dessus est caractéristique de l’opinion de certains investisseurs américains à la mi-99. Depuis, les cours n’ont pas cessé de monter, ce qui accroît encore leurs angoisses. Certaines des entreprises actives sur l’Internet, comme Amazon, n’ont apparemment jamais dégagé de profit[30]. D’autres, comme eBay, sont toutes récentes. Et cependant le marché les évalue en dizaines de milliards de dollars.

Certes, ces évaluations sont sans doute spéculatives, excessives etc. Certes, on peut ne pas être d'accord avec les managers qui se donnent pour seul but de « créer de la valeur[31] », ce qui dans leur langage signifie non produire des biens utiles aux consommateurs, mais faire monter le cours des actions de leur entreprise. Certes, le zèle des néophytes de l’Internet est irritant. On peut être excédé par les naïvetés qu’ils disent ou qu’ils font (et quand le naïf abonde, les escrocs pullulent), mais il ne faudrait pas jeter le bébé avec l'eau du bain.

Pourquoi les actionnaires, en masse, acceptent-ils de payer si cher (trop cher, certes) les actions des entreprises de l’Internet ? Beaucoup d'entre eux sont sans doute des moutons de Panurge, mais cela n'explique pas tout. Pourquoi vont-ils tous vers les NTIC (ou ce qui y ressemble, car dans ce domaine nouveau il est difficile de distinguer le sérieux du factice) ?

La réponse est simple : parce que les NTIC sont très efficace ; parce que le commerce électronique, c'est une bonne façon de faire du commerce ; parce que tout le monde pense, avec raison, que cette nouvelle forme de commerce va prendre une part significative du marché (pas 100 %, certes, mais il suffit de quelques dizaines de pour cent du commerce pour asseoir de belles entreprises).

___________

Nous allons nous efforcer de classer les idées concernant l’évaluation de la valeur des entreprises. Le développement qui suit s’enchaîne, par une sorte d’aiguillage, à la partie « définition de la fonction de coût » de l’annexe 1 précédente. Nous reprenons donc la numérotation des relations juste après le numéro (12) qui précédait cet aiguillage.

Le " price earning ratio " (PER) de l’entreprise est :

(13) PER = capitalisation boursière / profit (=) p_KK / rK (=) 1/(i + π) = 1 / TRI

Si l’on suppose enfin que le profit de l’entreprise croît au rythme annuel a, la VAN est égale à :

(14) VAN = - p_KK + (pY - wL) / (T - a), d’où le TRI :

(15) TRI = a + (pY - wL) / p_KK

Observons que l’équilibre que nous venons de décrire s’instaure sur des marchés obéissant à des dynamiques différentes. Plus un marché est large, plus la dynamique d’ajustement du prix en cas de déséquilibre sera lente toutes choses égales d’ailleurs, car elle nécessite la coordination d’un plus grand nombre d’acteurs.

La dynamique la plus rapide sera celle du cours de l’action, la moins rapide sera celle du salaire ; celle du prix du produit est intermédiaire.

1)     la capitalisation boursière de l’entreprise est à l’équilibre égale à la valeur de son profit futur anticipé, actualisé au taux (i + π). Elle varie si les actionnaires modifient leur estimation du profit anticipé ou si le taux d’actualisation change (que ce soit i ou π qui change). C’est sur ce marché fortement organisé que l’ajustement est le plus rapide (mais, comme les évaluations dépendent d’anticipations par nature incertaines, c’est aussi celui où l’ajustement est le plus incertain).

2)     le prix p du produit Y s’établit sur un marché sectoriel, qui recouvre une partie de l’économie. Il s’ajuste plus lentement que le prix de l’action, mais plus vite que le salaire.

3)     le salaire horaire w s’établit sur le marché du travail qui est macroéconomique (il est sectoriel si le secteur emploie des compétences spécialisées, ce que nous ne supposons pas ici). L’ajustement du salaire nécessite donc une coordination plus large, et c’est lui qui se fera le plus lentement.

Innovation incorporée au capital

Supposons que, par suite d’un progrès technique, le prix unitaire p_K des machines diminue de δp_K (ou, c’est équivalent, que la qualité des machines augmente de sorte que le même travail puisse être fait avec moins de machines, le prix nominal des machines restant constant) :

(16) p’_K = p_K - δp_K

Supposons qu’à court terme le prix p du produit et le salaire w ne sont pas modifiés, ces marchés obéissant à une dynamique lente.

A court terme l’entreprise n’est donc pas dans la situation d’équilibre résultant de la libre entrée, car atteindre cet équilibre suppose le moyen ou long terme ; elle dégage donc pendant le délai entre court et moyen-long terme un profit supérieur à celui qui rémunérerait normalement le risque pris par les actionnaires ; nous nommerons quasi rente ce surcroît de profit.

La quasi rente est supérieure à (i + π)δp_KK , car l’entreprise peut diminuer son coût de production par substitution du capital au travail ; donc, sur les nouveaux projets :

(17) pY > wL + (i + π)p’_KK + (i + π)δp_KK

La quasi rente est propriété des actionnaires, puisqu’ils sont propriétaires de l’entreprise et donc des profits qu’elle dégage. Ils sont libres de la répartir sous forme de dividendes ou de la réinvestir dans l’entreprise pour susciter une plus value durable.

La prime de risque apparente π’, supérieure à la prime de risque d’équilibre π, est pour les nouveaux projets :

(18) π’ > (i + π)p_K/p’_K - i

Des déséquilibres se manifestent alors sur plusieurs marchés. Ils suscitent à moyen terme des évolutions visant à restaurer les équilibres :

1)     si les actionnaires estiment durable l’accroissement du profit, le cours de l’action va croître. Les actionnaires anciens font une plus value « extra », supérieure à celle qui accompagne normalement l’autofinancement. Les nouveaux actionnaires, acheteurs d’actions « d’occasion », paieront leurs actions plus cher et bénéficieront seulement dans le futur de la prime de risque d’équilibre π.

2)     s’il y a libre entrée (ce que nous supposons), des entreprises nouvelles vont se créer, attirées par la rentabilité π’ du capital « frais » dans ce secteur. Cela fera diminuer le prix p.

3)     la quasi rente est constatée par les salariés. Ils vont dans les négociations réclamer un accroissement du salaire w. Ceci ne pourra toutefois avoir lieu que si la quasi rente s’étend à de nombreux secteurs en raison du caractère macroéconomique du marché du travail.

A moyen et long terme, si l’on suppose inchangés les déterminants de la prime de risque, les évolutions de p et éventuellement de w la ramèneront à son niveau d’équilibre et l’on retrouvera la norme de profit.

Le cours des actions correspondra alors à la prime de risque d’équilibre ; il reviendra au niveau antérieur augmenté de la plus value procurée par l’autofinancement.

Cette évolution inéluctable rend problématiques les anticipations de profit des actionnaires : il se peut qu’ils croient durable un niveau de prix qui ne pourra pourtant pas être maintenu. Dans ce cas, ils surestiment l’entreprise, et le retour à la normale s’accompagnera d’une baisse du cours de l’action.

A court terme, et dans l’attente des ajustements qui ramèneront les marchés vers l’équilibre, le partage de la valeur ajoutée se déforme en faveur des actionnaires : la diminution du prix p_K du capital entraîne en effet une substitution du capital au travail. A moyen long terme, le partage de la valeur ajoutée revient au niveau correspondant aux valeurs d’équilibre.

Innovation de procédé

Supposons que l’entreprise trouve un meilleur procédé de production : elle est capable de produire avec le même capital et le même travail une quantité Y’ > Y.

A court terme, le prix p et le salaire w ne changent pas. Il en résulte un accroissement du profit permettant de dégager une quasi rente :

(19) pY’ = wL + r’K, avec r’ > (i + π)p_K

On peut appliquer un raisonnement analogue au précédent, à quelques nuances près :

1)     l’innovation de procédé s’applique non aux projets nouveaux, mais à toute l’entreprise, puisqu’elle est supposée ne pas nécessiter de technique nouvelle. La nouvelle prime de risque concerne donc non les nouveaux projets, mais la totalité du capital qui se valorise d’autant.

2)     l’innovation de procédé est plus aisément mise en œuvre dans l’ensemble du secteur que l’innovation incorporée au capital : la dynamique d’ajustement du prix est plus rapide que celle induite par une innovation incorporée au capital.

3)     l’innovation de procédé entraîne à court terme un accroissement de la part du capital dans la valeur ajoutée, puisque les actionnaires perçoivent, outre la rémunération normale du capital, une quasi rente.

Observons enfin que dans les deux cas (innovation incorporée au capital ou innovation de procédé) la hausse immédiate de la prime de risque, qui entraîne rapidement une hausse du cours des actions, n’est que temporaire : la dynamique lente des prix et des salaires la ramène vers son niveau normal. Ainsi la quasi rente est éphémère : l’innovation, après avoir permis aux actionnaires de réaliser des plus values, finit par bénéficier aux consommateurs (par le biais des baisses de prix) et / ou aux salariés.

Si le flux d’innovations est renouvelé en permanence, l’écart peut toutefois se renouveler lui-même. Tant que le flux d’innovations se poursuit, le partage de la valeur ajoutée est plus favorable au capital qu’à l’équilibre, et les actionnaires perçoivent la quasi rente qui s’ajoute à leur rémunération normale.

On peut pour illustrer ce type de phénomène utiliser le formalisme de la croissance endogène (Romer[32], Arrow). Considérons un secteur où la fonction de production des entreprises est de Cobb-Douglas, l’un des facteurs de production étant l’expérience acquise A_t :

(27) Y_t = aK_t^αL_t^1-αA_t^γ

L’expérience est, comme le capital, une variable de stock ; dans un même secteur, on peut supposer les variables de stock corrélées au capital. Il est alors naturel d’approcher la mesure de l’expérience acquise par celle du capital.

L’expression de Y devient :

(28) Y_t = aK_t^αγL_t^1-α

Le rendement est alors croissant (1 + γ > 1), et on est nécessairement en situation de concurrence monopoliste (certains auteurs le pensent toutefois compatible avec la concurrence parfaite, le rendement croissant jouant selon eux au niveau sectoriel mais non à celui de l’entreprise considérée individuellement).

Supposons que la croissance endogène devienne plus rapide dans le secteur considéré. La part du capital dans la valeur ajoutée devient alors durablement supérieure, car d’après (22) :

(29) rK / pY = (αγ/(1 + γ), et α < 1.

Evolution de la capitalisation boursière

La rémunération « normale » d’une action, c’est TRI (=) i + π, où i est le taux d’intérêt du marché et π la prime de risque caractérisant l’entreprise considérée. (10) et (11) fournissent la valeur d’équilibre de la prime de risque. Si l’entreprise est endettée, la prime de risque et le risque lui-même sont modifiés par l’effet de levier ; toutefois un actionnaire rationnel doit corriger cet effet pour évaluer l’entreprise : pour son propre arbitrage entre rendement et risque, il est indifférent que ce soit l’entreprise ou lui-même qui s’endette.

La capitalisation boursière d’une entreprise, c’est-à-dire la valeur que lui attribue le marché boursier, c’est la valeur anticipée de ses profits futurs actualisés par le TRI « normal ». L’anticipation des profits comporte une incertitude que la prime de risque a pour rôle de rémunérer. Cette anticipation peut en outre, si l’actionnaire fait une erreur de jugement (hypothèse que l’on ne peut exclure s’agissant d’anticipations), comporter un biais qui altère l’évaluation de l’entreprise.

Lorsque se produit une innovation incorporée au capital, ou une innovation de procédé, ou encore une accélération de la croissance endogène, le délai d’ajustement des prix ouvre un intervalle de déséquilibre favorable au profit, donc aux actionnaires. Le marché qui s’ajustera le plus vite, avant que les autres marchés ne soient en équilibre, c’est le plus volatil, celui des actions. La valeur de l’action croîtra dans des proportions diverses selon que le marché perçoit la hausse du profit comme :

-         temporaire (« bosse » avant retour au niveau antérieur),

-         durable (« marche d’escalier » portant le profit à un niveau où il restera),

-         extrapolable (l’accroissement récent se prolongera).

Durant cet intervalle de déséquilibre, l’évaluation des actions est difficile. Si le phénomène touche plusieurs secteurs et plusieurs entreprises, le marché peut avoir des anticipations optimistes et exiger en outre de toutes les entreprises (y compris de celles qui ne dégagent pas de quasi rente) des profits élevés. L’évaluation des entreprises s’écarte de la mesure de leur actif net, les entreprises jugées obsolètes subissant une dépréciation, les entreprises innovantes bénéficiant d’une valorisation.

La hausse du profit est synonyme d’une modification du partage de la valeur ajoutée en faveur des actionnaires : étant propriétaires de l’entreprise, ils sont propriétaires du profit qu’elle dégage. S’il n’y avait pas de fluctuation du partage de la valeur ajoutée, donc du profit, la capitalisation boursière croîtrait comme le capital des entreprises, donc comme le PIB si l’on suppose le flux de valeur ajoutée proportionnel au capital.

A terme toutefois, la concurrence et la libre entrée entraînent un ajustement des prix (baisse de p d’abord, puis hausse éventuelle de w) ramenant la rémunération du capital à son niveau normal. La capitalisation boursière des entreprises redevient égale à la valeur de leur actif net. L’innovation a apporté aux actionnaires une « bosse » temporaire de revenu, mais finit par bénéficier aux consommateurs et aux salariés à travers la baisse du prix, et éventuellement la hausse du salaire.

Le cours des actions revient à son niveau initial, accru toutefois des plus values accumulées par autofinancement. La quasi rente a disparu. Les actionnaires qui ont acheté lorsque les cours étaient élevés sont évidemment les grands perdants de cette histoire.