Le métier de statisticien

Les grandes articulations

Dans sa pratique, le travail de production statistique est étonnamment peu mathématique. Son outil de calcul essentiel est la règle de trois, dont il est fait un usage abondant pour estimer, extrapoler, ventiler, calculer des indices, etc. L'expérience montre d'ailleurs que, malgré sa grande modestie intellectuelle, la règle de trois n'est pas d'un usage aussi facile qu'on pourrait le croire (1). Mais il y a loin, de toute façon, entre la formation mathématique poussée que reçoit le statisticien, et les travaux qu'il aura à réaliser pratiquement dans son métier. Les questions auxquelles il aura à répondre seront le plus souvent les suivantes : " Comment rédiger le questionnaire, avec ses notes explicatives et ses définitions ? Quelles instructions donner aux enquêteurs pour la collecte et la vérification ? Comment préparer l'exploitation ? Comment présenter la publication finale ? " Il aura aussi à se préoccuper d'organisation du travail, à négocier avec d'autres services, notamment avec les services informatiques. On peut être un excellent statisticien sans jamais calculer une seule variance, un seul " intervalle de confiance " ; on ne se réfère au calcul des probabilités, et encore sous sa forme la plus élémentaire, que pour résoudre certains problèmes de sondage. La critique et la publication des résultats nécessitent que l'on connaisse bien quelques " trucs " de lecture ou de présentation : certains praticiens développent ici un flair professionnel qui leur permet de repérer avec une rapidité étonnante des anomalies dans un grand tableau, ou d'imaginer des graphiques particulièrement " parlants ". Mais il y a loin entre ces astuces de métier et les raffinements logiques de la statistique mathématique. Cette discipline, qui s'est développée au XIXe siècle en relation étroite avec un volumineux travail de collecte (2), s'en est depuis séparée. On peut le déplorer. L'effort d'organisation théorique des mathématiciens n'aurait été que plus fécond, nous semble-t-il, s'il avait porté sur les problèmes rencontrés par les praticiens de la statistique ; ceux-ci, de leur côté, auraient tout intérêt à compléter et à contrôler les indications que leur fournit leur expérience professionnelle, en utilisant des instruments logiques rigoureux. Il se peut qu'il y ait sur ce point une évolution, facilitée par la grande capacité de calcul automatique procurée par les ordinateurs ; le développement de l'analyse des données, notamment, marque peut-être le début de l'introduction de procédures logiques affinées (sinon véritablement complexes) à l'intérieur même de la production statistique. Pour le moment, en tout cas, nous n'en sommes pas là ; et, pour se convaincre de l'écart existant entre la pratique statistique et la statistique mathématique, il suffit de parcourir des livres portant sur l'une et l'autre de ces discipline (3).

Ainsi les outils conceptuels de la pratique statistique, son langage, n'ont avec les mathématiques qu'un rapport assez éloigné. La statistique a un vocabulaire propre ; elle repose sur quelques " évidences ", souvent implicites, partagées par tous les praticiens. Pour comprendre ce qu'elle est et bien apprécier les problèmes qu'elle pose, il faut entrer dans cet édifice et en acquérir une certaine familiarité. Nous nous efforcerons de donner dans cette partie une présentation de la pratique statistique qui, sans aller jusqu'à la méticulosité parfois un peu pédante des traités spécialisés, procurera au lecteur une approche suffisamment précise pour notre propos. Il pourra ainsi, lorsque nous considérerons dans les parties suivantes la statistique sous les angles historique et politique, se rappeler le contenu concret de sa démarche, les procédures à l'aide desquelles elle met effectivement en œuvre les schémas conceptuels sur lesquels elle est fondée. La statistique, comme les autres instruments d'observation, opère une articulation délicate entre un cadre logique conçu a priori et le réel observé dans ce cadre et selon ses découpages ; il y a là, si nous pouvons oser cette expression qui d'ailleurs parle d'elle-même, une sorte d'incarnation de la logique qu'il est intéressant de suivre dans ses diverses étapes.

Dans les applications, la statistique porte sur des domaines variés et l'adaptation à chaque domaine nécessite l'usage de techniques très diverses : enquêtes exhaustives ou par sondage, collecte par enquêteur ou par voie postale, exploitation de documents administratifs. etc. L'" individu statistique " peut être choisi de multiples façons ; une enquête mensuelle ne se traite pas comme une enquête annuelle, ni comme un recensement ; à chaque type d'enquête correspond une organisation du travail particulière. La panoplie des techniques est donc large, et sa description complète excéderait le cadre de ce travail. Nous préférons, pour faire entrer le lecteur " dans l'intérieur " d'une opération statistique, suivre les étapes d'une opération fictive où l'on retrouve les caractéristiques essentielles de la pratique. Chemin faisant, nous évoquerons quelques variantes, de façon à élargir la portée de cette description.

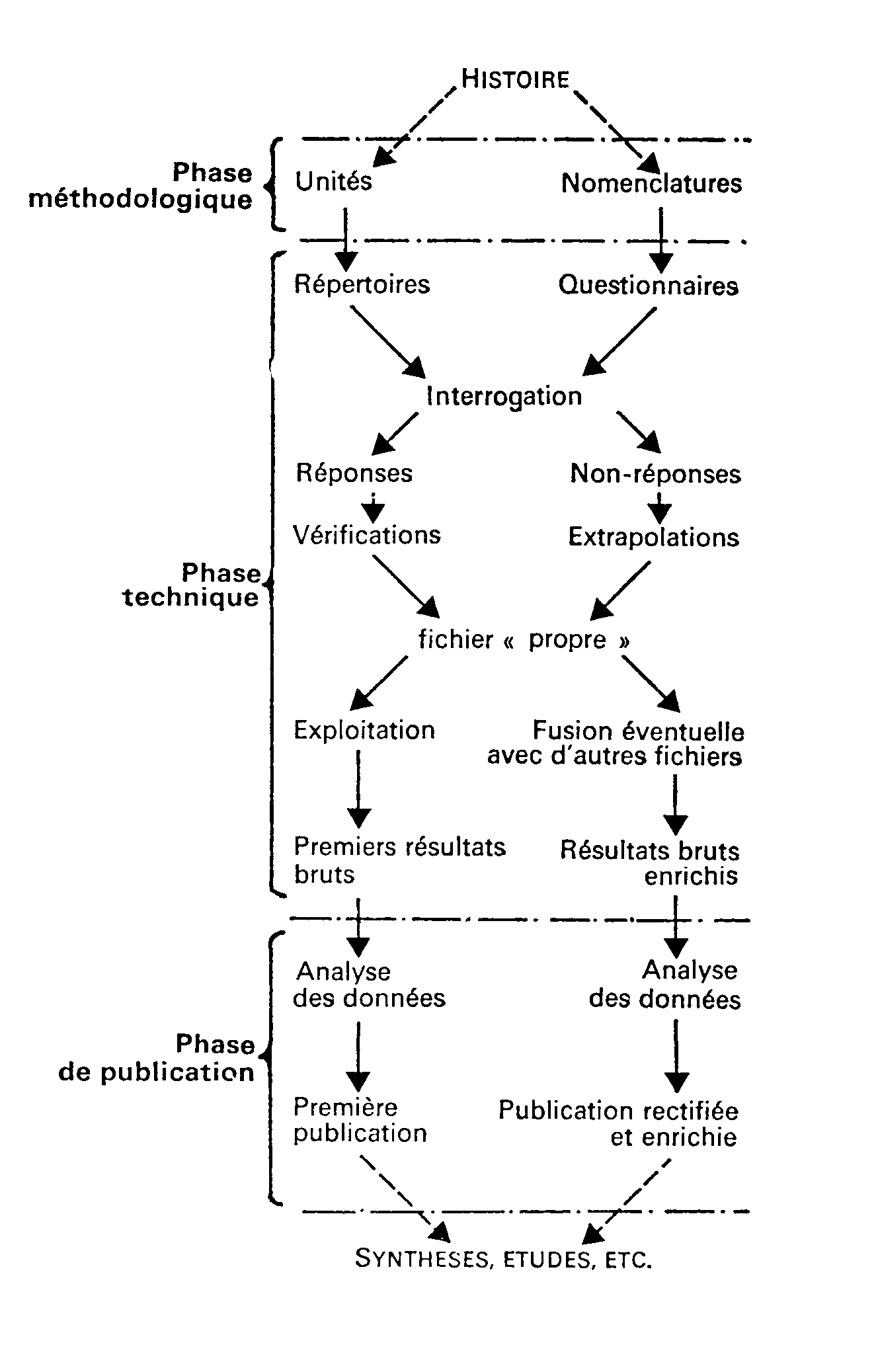
Les diverses étapes d'une opération statistique peuvent être réparties en trois phases distinctes, conformément au schéma de la p. 30 ; lors de la " phase méthodologique " sont choisis le découpage conceptuel et les définitions qui fondent l'instrument. La " phase technique " est celle de la mise en œuvre, de l'observation proprement dite. La " phase de publication " qui vient ensuite est celle où l'on confectionne, à partir du résultat brut de l'observation, un texte compréhensible pour l'utilisateur final. A chacune de ces phases sera consacré un chapitre qui permettra de bien comprendre ce qui se trouve derrière les cases du schéma.

Le conditionnement historique de la statistique, qui détermine les " besoins d'information " et leur incidence sur l'instrument d'observation, sera évoqué dans la deuxième partie. Les utilisations de la statistique (synthèses, études, etc.) seront l'objet de la troisième partie. Les traits en pointillé sur le schéma représentent donc des relations qui ne seront pas examinées immédiatement ; et le lecteur dont l'intelligence va plus vite que le texte, et qui, à bon droit, demande : " Pour qui tout cela est-il fait ? A quoi cela sert-il ? " devra attendre, avant de recevoir une réponse, d'avoir vu en quoi " cela " consiste.