|
Correction des variations saisonnières
(voir système
de pilotage de l'entreprise)
Les séries chronologiques sont souvent caractérisées par des
inflexions saisonnières. L’interprétation d’une série chronologique qui
comporte un mouvement saisonnier exige que l’on procède à une
" correction des variations saisonnières " : sans quoi ce sera
l’interprétation elle-même qui sera saisonnière, et chaque année on aura
l’impression que " ça monte " à la même date, que
" ça baisse " à la même date. Ce qui importe, c’est de savoir
si " ça monte " ou " ça baisse " plus ou moins
que d’habitude, c’est-à-dire d’évaluer la tendance sous-jacente.
Forme de l’équation
S’il existe un phénomène saisonnier, l’observation
relative au mois m de l’année a prend la forme :
Xma = Tma + Sm + ema
où Tma est la tendance sous-jacente, insensible au
mouvement saisonnier, Sm le facteur saisonnier, et ema un terme aléatoire.
On peut aussi supposer que le mouvement saisonnier est
multiplicatif, en retenant la spécification suivante :
Xma = Tma Sm( 1+ ema)
Il est équivalent d’utiliser cette dernière
spécification, ou d’appliquer la spécification additive aux logarithmes des
variables considérées. Des tests permettent de choisir la spécification la plus
convenable pour le cas considéré.
(Dans les paragraphes ci-dessous, nous utiliserons
indifféremment les notations t ou ma pour désigner le mois courant).
Jours ouvrables
La durée du mois sera prise en compte par le coefficient
saisonnier, sauf en ce qui concerne le mois de février qui a un jour de plus une année
sur quatre.
Certaines activités économiques sont très sensibles au nombre
de jours ouvrables dans le mois. Ce nombre dépend de la durée du mois, mais aussi du
nombre de week-ends, des jours fériés etc. Il convient dans ce cas de faire passer une
première correction portant sur le nombre de jours ouvrables.
Élimination des mois aberrants
Il convient de corriger les données relatives aux mois pendant
lesquels s’est produit un événement exceptionnel (grève, guerre du golfe, etc.).
Pour cela, on établira un graphique sur lequel on superpose les courbes relatives aux
diverses années, et on corrige " à l’oeil " (en fait ces
corrections sont assez précises) les données relatives aux mois aberrants. C’est
sur les données ainsi retouchées que se fera ensuite la correction des variations
saisonnières.
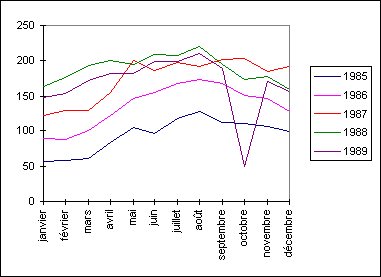
Données comportant un mois aberrant en octobre 1989
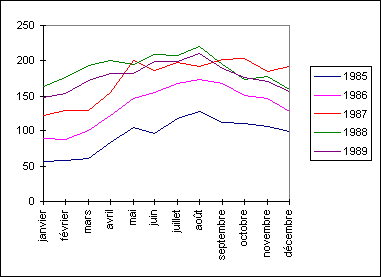
Données après correction du mois aberrant
Calcul des coefficients saisonniers
Pour estimer les coefficients Sm, il faut disposer
d’une série mensuelle assez longue (au moins quatre ans).
On commence par affecter à chaque mois une moyenne mobile sur
douze mois (MM12). On peut utiliser une formule du type suivant :
Mt = (Xt-6/2 + Xt-5 + Xt-4
+ Xt-3 + Xt-2 + Xt-1 + Xt + Xt+1 +
Xt+2 + Xt+3 + Xt+4 + Xt+5 + Xt+6/2)/12
(en fait le choix des coefficients est libre, l’essentiel
est d’avoir une moyenne centrée sur le temps t et portant sur douze mois).
Le calcul de la MM12 ne peut démarrer que sur le septième mois
connu, puisqu’il faut pouvoir commencer à t - 6. On " perd "
donc dans ce calcul les six premiers et six derniers mois. Si l’on dispose de
données sur quatre ans, on ne pourra calculer la MM12 que sur trois ans.
On calcule ensuite les écarts entre Xt et Mt
Et = Xt - Mt
et on estime le coefficient saisonnier Sm par Um
:
Um = (1/n) SaEam
où n est le nombre d’années sur lesquelles on a mesuré
les écarts Et.
La série CVS est ensuite estimée en calculant :
Cam = Xam - Um
Observons que le terme aléatoire et reste présent dans l’expression de la série CVS,
qui ne cherche pas à corriger l'aléa, mais seulement l'effet saisonnier.
Exemple
La série brute ci-dessous a été obtenue de façon
artificielle, en additionnant une tendance (d’abord croissante, puis décroissante),
un mouvement saisonnier et un bruit blanc.
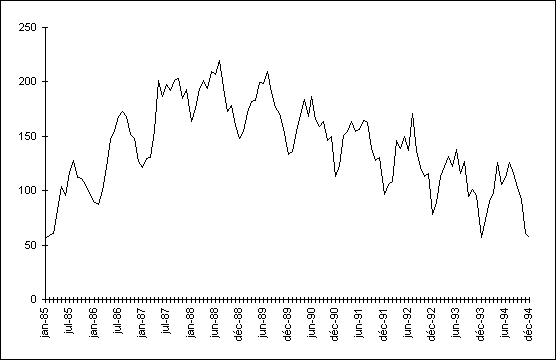
On obtient le résultat ci-dessous en appliquant à cette série
la technique de CVS que nous avons décrite :
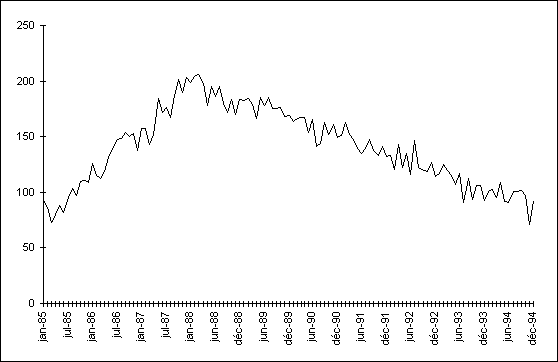
Les effets saisonniers sont pratiquement éliminés. Il reste
l’effet du bruit blanc, ce qui n’interdit pas d’identifier les tendances et
de repérer avec une précision satisfaisante la date du retournement (janvier 1988).
|