|
Durée de vie d’un logiciel
16 avril 2000
Le but de cette fiche est de
proposer une modélisation de la durée de vie d’un logiciel. Nous
considérerons d’abord le cas le plus simple, puis nous introduirons des
hypothèses relatives à la modularité du logiciel, ainsi qu’à l’évolution
tendancielle du coût du développement.
La modélisation suppose que l’on
simplifie la description pour ne retenir que quelques hypothèses essentielles.
Il ne serait donc pas recommandé d’utiliser tels quels les résultats
quantitatifs du modèle. Ils sont moins intéressants par eux-mêmes que par les
indications qualitatives qu’ils fournissent.
Notons n la taille d’un
logiciel, qu’elle soit mesurée par le nombre de lignes de code ou de points
de fonction ou par toute autre unité : ces diverses mesures de la taille
sont toutes approximativement proportionnelles.
La complexité du logiciel est
f(n), fonction croissante de la taille du logiciel (nous n'avons pas besoin pour
notre raisonnement de spécifier davantage cette fonction).
Notons n0 la taille
initiale du logiciel. Nous supposons son coût initial C0 de
production proportionnel à sa complexité :
C0 = kf(n0)
Une fois le logiciel en service,
des travaux de maintenance seront ultérieurement nécessaires pour l’adapter
aux modifications de l’environnement technique (architecture de la
plate-forme, nouvelles versions des systèmes d’exploitation, etc. : nous
ne parlons pas ici de la " maintenance évolutive ", qui
consiste à introduire de nouvelles fonctionnalités et doit donc être
considérée comme un nouveau développement).
Les travaux de maintenance
conduisent à écrire de nouvelles lignes de code qui s’ajoutent aux lignes
initiales. La taille du logiciel croît donc au fur et à mesure de son
vieillissement, ainsi que sa complexité. Supposons que le coût annuel de la
maintenance soit celui de la croissance de la complexité du logiciel :
mt = kDf(nt)
Supposons que ce coût soit égal
au coût cumulé du logiciel (y compris les coûts de maintenance
antérieurs), multiplié par un coefficient p. On a alors à l'année t :
mt =
pkf(nt)
Il en résulte que :
Df(nt)/f(nt)
= p, d'où :
f(nt)
= f(n0)ept
le coût annuel de la maintenance est donc
:
mt = pC0ept
La série des coûts annuels est
la suivante, si l’on suppose le coût de production initial C0
dépensé pendant la première année :
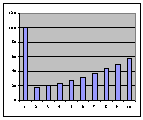
Graphique 1
Le coût de maintenance augmente
exponentiellement avec le temps. Il sera donc préférable, au bout d’un
délai, de refaire le logiciel à neuf : ce délai sera appelé
" durée de vie du logiciel ". Le but du calcul ci-dessous
est d'évaluer la durée de vie optimale du logiciel.
Supposons que l’entreprise
retienne le taux d’actualisation r, et que la durée de vie du logiciel soit
d. A la fin de la durée de vie, le logiciel est entièrement refait pour le
même coût C0, et le cycle reprend.
Le coût actualisé du logiciel
sur un cycle de vie est :
A = C0 (1 + pò0->d e(p – r) tdt)
Soit, si p # r,
A = C0 [1 + p(e(p
– r) d - 1)/(p – r)]
L’annuité équivalente à
cette dépense est par ailleurs a tel que :
A = aò0->d e – r tdt
= (1 – e–rd)/r
D’où :
a = rC0 [1 + p(e(p
– r) d - 1)/(p – r)]/(1 – e–rd)
La durée de vie qui minimise a
est d* tel que :
p(r – p)e(p + r)d* =
r2erd* - p2epd*
Il n’est pas possible de
trouver la solution analytique de cette équation ; on peut cependant la
trouver par un calcul numérique. Supposons que p = 15 % et r = 9 %
(valeurs classiques), on trouve :
d* = 7,2 ans
l'annuité équivalente
correspondante est a*, minimum de a :
a* = 0,44C0
Le graphique ci-dessous indique
la valeur de a pour différentes durées de vie du logiciel.

Graphique 2
Le tableau ci-dessous donne les
valeurs de la durée de vie d* pour divers taux d’actualisation r et taux de
maintenance p :
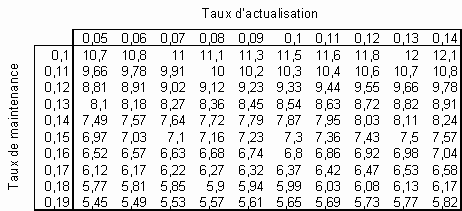
Tableau 1
Le logiciel sera refait à neuf
toutes les d* années ; la chronique des dépenses annuelles aura donc non
l’allure indiquée par le graphique 1, mais l’allure suivante :
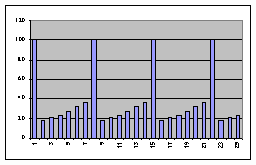
Graphique 3
On observe que le coût de
maintenance est, à la fin de la durée de vie, égal à 0,37C0 : ceci
(conjugué au fait que nous avons choisi pour p et r des valeurs
"réalistes") explique une " règle de pouce " d’usage courant :
" il faut refaire le logiciel lorsque le coût de maintenance atteint
le tiers du coût de réfection ".
Modularité du logiciel
Supposons que nous retenions pour
mesurer la complexité la fonction f(n) = n2, qui est
approximativement proportionnelle à n(n - 1)/2, nombre de couples
d'instructions du logiciel, on trouve :
f(q) + qf(n/q)
= q2 + n2/q » n2/q
La complexité d’un logiciel
modulaire est donc égale à la complexité d’un logiciel non modulaire de
taille équivalente, divisée par le nombre de modules.
Le coût de production d’un
logiciel modulaire est toutefois analogue à celui d’un logiciel non modulaire
(donc proportionnel à n2), car la conception des modules suppose l’examen
des n éléments du programme. Par contre le coût de maintenance bénéficiera,
lui, des économies permises par la modularité.
Il en résulte que la durée de
vie d’un logiciel modulaire est égale à celle d’un logiciel non modulaire
de même coût de production, mais dont le coût de maintenance, mesuré par le
coefficient p dans (10), serait divisé par q. La durée de vie du logiciel
modulaire est alors d* tel que :
(p/q)(r – p/q)e(p/q + r)d*
= r2erd* - (p/q)2e(p/q)d*.
Supposons que p = 15 %, r =
9 % et q = 10 ; on trouve alors :
d* = 131ans, a* = 0,1C0
Ce qui signifie que la durée de
vie du logiciel est pratiquement infinie. Dans le monde réel, la durée de vie
d’un logiciel n’est bien sûr jamais infinie parce que les exigences du
métier qu’il doit satisfaire évoluent ; l’obsolescence n’est plus
alors d’origine technique, mais d’origine fonctionnelle, et elle relève d’un
autre type d’analyse.
Un degré supérieur de la
modularité est atteint par les logiciels orientés objet, qui poussent cette
économie au maximum.
Diminution tendancielle du coût
de réfection
Revenons au cas d’un logiciel
non modulaire, et supposons que le coût de réfection diminue dans le temps au
rythme s, en raison par exemple des progrès des langages de programmation.
Au cycle de vie de rang c du
logiciel, on peut associer un coût Ac :
Ac = Ae-scd
Où d est la durée de vie, et
où cd représente donc le nombre d’années écoulées avant le cycle de rang
c.
Le coût actualisé de la
succession des cycles est :
C =
Sc=0->¥ e–rcdAc
= AS c=0->¥
e–(r+s)cd = A/(1 - e–(r+s)d)
L’annuité équivalente à
cette dépense est a tel que :
C = a/r
D’où :
a = r C0 [1 + p(e(p
– r) d - 1)/(p – r)]/(1 - e– (r + s)d)
Si l’on suppose que p = 15 %,
r = 9 % et s = 10 %, on trouve :
d* = 5,4 ans, a* = 0,27C0
La baisse du coût de réfection
a donc pour effet de diminuer la durée de vie du logiciel. La chronique des
dépenses annuelles a l’allure suivante (comparer avec le graphique
3) :
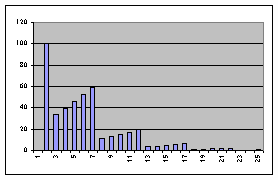
Graphique 4
Conclusion
Lorsque l’on considère l’économie
d’un système d’information, il est important de tenir compte de la durée
de vie des logiciels : elle a une incidence sur leur coût si on considère
non seulement leur coût de réalisation, mais aussi leur coût de maintenance
(un calcul complet doit aussi prendre en compte leur coût d’exploitation,
mais ce n’était pas notre objet ici car toutes choses égales d’ailleurs le
coût d’exploitation n’a pas d’incidence sur la durée de vie). Ce qui
compte du point de vue économique en effet, c’est plus l’annuité
équivalente que le coût de production ; on notera cependant que l’évaluation
de l’annuité équivalente dépend du taux d’actualisation retenu, et
comporte donc une hypothèse qu’il convient de justifier soigneusement.
Il faudra considérer l’évolution
des coûts de réfection et tenir compte de la réduction du coût de
maintenance procurée par la modularité du logiciel.
Au total, on peut résumer les
résultats ci-dessus en associant au logiciel un coût de production, un coût
de maintenance en pourcentage du coût de production, et une durée de vie. En
procédant ainsi, on efface bien sûr toute trace de la croissance tendancielle
du coût de maintenance qui a servi de fondement au calcul de la durée de
vie ; cette simplification se justifie par le fait que l’entreprise
utilise simultanément des logiciels d’âges divers, et que le coût de
maintenance unitaire d’ensemble est une moyenne des coûts de maintenance de
ces logiciels.
|