Éléments d’économétrie

(voir système de pilotage de l'entreprise)

Le but de cette fiche est de donner les éléments essentiels permettant de comprendre les méthodes de l’économétrie et d’interpréter ses résultats sans faire d’erreur grave.

Nous donnons d’abord quelques exemples illustrant l’apport de l’économétrie. Puis nous donnons ses propriétés mathématiques essentielles, et enfin examinons la présentation de ses résultats.

Ce résumé correspond assez bien à la pratique empirique des modélisateurs ; une pratique " rigoureuse " demanderait d’autres précautions ; elle est en fait assez rare, car elle nécessite beaucoup plus de travail pour un gain faible en ce qui concerne la qualité des résultats.

Quelques exemples

On constate après 1973, dans les comptes nationaux, un ralentissement de l’investissement des entreprises. Mais, sur la même période, leur production a ralenti aussi. Doit-on considérer que le ralentissement de l’investissement est fort ou faible ? Il faut pour cela :

1) avoir une explication théorique de l’investissement, qui le relie à des variables explicatives (ici : variation de la production et rythme des déclassements) ;

2) avoir spécifié cette explication sous la forme d’une équation se prêtant au calcul, ici :

(1) I_t = c ΔQ_t + ac Q_t-1

3) avoir estimé les paramètres de cette équation par ajustement sur les séries statistiques observées (ici : a = 3,5 % et c = 1,4 sur la période 1963-1973).

Après quoi l’on peut répondre à la question. En l’occurrence, il apparaît que l’investissement a moins baissé que ne l’impliquait le ralentissement de la production : on peut donc dire que, contrairement aux apparences, le comportement d’investissement a été soutenu.

Seule l’économétrie, avec ses trois étapes (explication, spécification, estimation), a permis de répondre à la question.

Supposons qu’une entreprise diminue son prix de vente. Cette mesure a deux effets de signe contraire : augmentation des ventes en volume, baisse du prix unitaire. Seule l’estimation de l’élasticité de la consommation au prix, réalisée sur les séries chronologiques disponibles, permet d’éclairer cette question.

L’élasticité prix est :

(2) η = (p/Q) ∂Q/∂p

η est le plus souvent négative. Si 0 > η > -1, l’effet d’une hausse de prix sera d’augmenter le chiffre d’affaires. Si η = -1, le chiffre d’affaires est indépendant du prix. Si η < -1, une hausse du prix fait diminuer le chiffre d’affaires.

On voit ici que le calcul (quantitatif) est indispensable pour conduire jusqu’au bout un raisonnement qualitatif : sans estimation de l’élasticité, il est impossible de prévoir le signe de l’effet d’une modification du prix sur le chiffre d’affaires.

La théorie économique, notamment la macro-économie, comporte un riche catalogue de spécifications : fonctions de Houtthaker-Taylor pour la consommation, de Cobb-Douglas pour la production, de Bischoff pour l’investissement, etc. Le choix des spécifications est varié (choix des variables et de leur forme : en niveau, en taux de croissance, logarithmes, variations, quotient de variables, variables retardées etc.). La finesse et la cohérence théoriques sont ici les critères essentiels. On doit tenir compte aussi des limites des statistique disponibles.

La tâche propre de l’économétrie est d’estimer les paramètres des équations par ajustement sur les séries passées. L’ajustement conduit parfois à réviser la spécification : lorsqu’une variable " ne sort pas " (coefficient non significatif, cf. ci-dessous), ou qu’elle a un coefficient du " mauvais signe " (effet contraire à celui théoriquement attendu).

L’économétrie ne donne que des indications, non des preuves : on ne peut pas dire qu’une spécification a été " prouvée ", mais seulement qu’elle n’a pas été rejetée par les tests. L’usage de ses résultats doit donc être prudent.

On prend cependant un risque lorsque l’on retient une hypothèse rejetée par l’économétrie (par exemple sur les élasticités). Celui qui procède ainsi doit indiquer pourquoi il s’estime autorisé à passer outre.

Régression

Supposons que l’on ait spécifié une relation qui explique la variable Y (repérée par une série chronologique, t varie de 1 à T) par un ensemble de p variables explicatives, que nous noterons X¹, ..., X^p. Nous noterons X^k la variable explicative courante (k = 1, ...,p).

L’équation à estimer est :

(3) Y_t = a₁X¹_t + a₂X²_t + ... + a_p X^p_t, ou

(4) Y_t = Σ_k a_kX^k_t

A chaque ensemble des T observations relatives à une variable peut être associé un vecteur de l’espace à T dimensions. Supposons que p = 2 ; on peut avoir une situation de ce type :

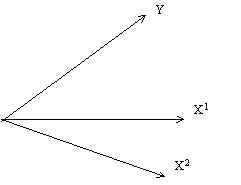
X¹ et X² définissent un plan. Si Y appartenait à ce plan, tout serait facile : les coefficients a_k seraient les coordonnées de Y dans la base formée par X¹ et X². On les obtiendrait par un calcul simple.

Dans le cas général, Y n’appartient pas au plan formé par X¹ et X² ; l’" explication " de Y par X¹ et X² est " incomplète ". Il peut y avoir des erreurs de mesure, des aléas, ou encore la spécification a négligé une variable explicative importante.

Lors de la phase d’ajustement, on pose par hypothèse que la spécification est vraie (quitte à tester cette hypothèse par la suite). On fait donc comme si la seule raison pour laquelle Y n’appartient pas au plan résidait dans des erreurs de mesure sur Y, ou dans des aléas statistiques.

S’il n’y avait pas d’erreur, on aurait trouvé :

(5) Y*_t = Σ_k a_kX^k_t

les a_k étant les coefficients vrais.

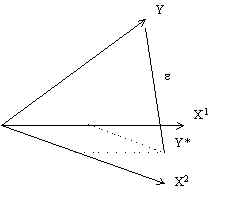
Le " vecteur des erreurs " ε a pour coordonnées ε _t = Y_t - Y*_t.

On ne connaît pas Y*, mais seulement Y. On va estimer Y*. La solution qui se présente le plus naturellement à l’esprit est de prendre le point du plan (X¹, X²) le plus proche du point observé Y : nous noterons ce point Y. C’est la projection orthogonale de Y sur le plan (X¹, X²).

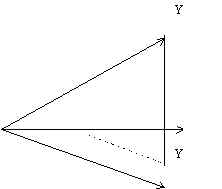
Les programmes de calcul permettent de trouver les coordonnées a_k du point Y dans le plan. Ces coordonnées sont les estimations des paramètres de la relation (4).

Commentaires

1- Il n’y a généralement pas de raison de supposer que le vecteur e est allongé dans une direction de l’espace plutôt que dans une autre. La projection de Y en Y se fait alors selon la définition canonique de l’orthogonalité : elle correspond à la distance euclidienne canonique, (distance)² = Σ (différence des coordonnées)². On dit que l’on utilise les " moindres carrés ordinaires " (MCO).

Dans certains cas, on doit supposer qu’il existe entre les coordonnées de e des relations telles qu’il risque de se trouver plutôt dans certaines directions de l’espace : sa distribution de probabilité n’est plus sphérique, mais ellipsoïdale.

On utilise alors une métrique particulière, selon la méthode des " moindres carrés généralisés " (MCG). Elle est notamment utile lorsque ε _t est fortement corrélé avec ε _t-1. Le test de Durbin et Watson (cf. ci-dessous) permet de savoir si l’on est dans ce cas.

2 - les variables X^k peuvent être presque colinéaires (il existe, dans le paquet des p vecteurs X^k, des vecteurs faisant un angle petit). La détermination des coefficients a_k est alors entachée d’une imprécision. Le test de Student (cf. ci-dessous) permet de savoir si l’on est dans ce cas.

3 - l’économétrie comporte des raffinements, mais la plupart du temps les choses se passent simplement : on estime les a_k par MCO, et on ne fait autrement que si le test de Durbin et Watson est mauvais, ou si le test de Student est mauvais pour une variable importante. Des méthodes préprogrammées dans les logiciels d’économétrie permettent alors de s’en sortir.

Complément : présentation du résultat d’une régression

Le résultat d’une régression peut avoir une forme apparemment compliquée, pour peu que le nombre des variables soit élevé.

Considérons l’équation " partage de l’offre " du modèle METRIC, qui répartit l’offre industrielle totale entre production et importations. La présentation est très technique :

X = XI/(XI + IMI) = 0,773 + 30,2/(T + 90) + 0,1 CAPA + Σ _{0≤ i≤ 5} a_i PXI/PIMI

                          (24,1)    (15,0)              (2,8)

a₀ = - 0,032 a₁ = - 0,034 a₂ = - 0,034 a₃ = - 0,030 a₄ = - 0,023 a₅ = - 0,01

            (3,5)          (7,6)             (9,3)            (6,5)              (5,0)          (4,2)

R² = 0,99

DW = 1,55

SEE = -0,0033 (moyenne de X = 0,83)

Période d’estimation : 1965 à 1976

où les notations signifient :

XI : production industrielle

IMI : importations industrielles

T : temps

CAPA : marges de capacité disponibles

PXI : prix de la production industrielle

PIMI : prix des importations industrielles

Les coefficients a_i décrivent une structure de retard sur le rapport des prix relatifs production/importation.

Cette équation traduit trois idées a priori : 1) ouverture tendancielle du marché aux produits étrangers ; 2) on importe d’autant plus qu’il y a plus de tension sur les capacités de production ; 3) on importe d’autant plus que les prix de production sont élevés par rapport aux prix des importations.

Voici l’explication des indications techniques :

En dessous des estimations des coefficients figure entre parenthèses le test de Student. En pratique, il faut que ce test soit supérieur à 1,75 pour que l’on puisse dire que le coefficient est significativement différent de zéro. C’est le cas pour ceux de cette équation.

R² = 0,99 : le R² est le cosinus carré de l’angle entre Y et Y. Plus il est proche de 1, plus Y est allongé sur le sous espace engendré par les vecteurs X^k. Si l’on a affaire à des séries chronologiques, le R² est souvent très fort sans que cela signifie grand chose, car beaucoup de séries croissent avec le temps. Par contre, il faudra s’interroger si le R² est faible (disons inférieur à 0,6).

DW = 1,55 : c’est le test de Durbin et Watson. Il sert à vérifier si le vecteur des erreurs est distribué indifféremment dans l’espace. DW doit être situé entre 1,5 et 2,5 pour que l’on puisse dire que les MCO sont légitimes. On s’inquiétera si DW < 1 (autocorrélation positive des erreurs) ou DW > 3 (autocorrélation négative).

SEE = 0,0033 : c’est l’écart type de l’erreur qui affecte la variable expliquée. En le divisant par la moyenne des X (ici 0,83), on obtient une idée de la précision de la régression (ici 0,4 %).

Période d’estimation : indique l’intervalle (1, ..., T) sur lequel les séries ont été observées. C’est une indication importante : bien souvent, les paramètres changent lorsque l’on change de période d’estimation. La pérennité des " lois économiques " que l’on estime par l’économétrie est donc souvent limitée.