Le but de cette fiche est de décrire les effets de chocs démographiques bien spécifiés :
- allongement de la durée de vie,
- baisse de la fécondité,
- « Baby-Crash » suivi d'un « Baby-Boom » (baisse temporaire de la fécondité suivie d’une hausse compensatrice de durée équivalente).

Nous examinerons d'abord trois variantes pour explorer les conséquences de tels chocs sur une population de structure très simple. Puis nous nous rapprocherons du réalisme (sans chercher à l'atteindre toutefois) en simulant une combinaison de chocs semblable à ceux qu'a subis la France.

Nous verrons ainsi qu'un choc a priori simple et ponctuel peut susciter une dynamique longue d'allure complexe, ses effets se propageant d'une génération à l'autre comme une onde qui s'amortit progressivement. On peut, si l'on oublie ce phénomène, être tenté d'attribuer à cette évolution une cause conjoncturelle inexistante.

Cet exercice montre que la statistique est fallacieuse, malgré sa prétention à l'objectivité, si elle reste le nez collé sur les données et ne les associe pas à un modèle qui permette de les interpréter.

Trois variantes

Nous partirons d’une population fictive stationnaire présentant des caractéristiques simples : la durée de vie est supposée constante et égale à 70 ans ; la période de fécondité se situe entre 20 et 40 ans, la période d’activité entre 20 et 60 ans ; la fécondité est constante et assure exactement le renouvellement de la population. On suppose que ce régime de croissance a été suivi pendant assez longtemps pour que la pyramide des âges ait atteint sa forme stationnaire, qui est cylindrique. Nous supposons qu’alors l’effectif de chaque classe d’âge quinquennale est de 10 millions.

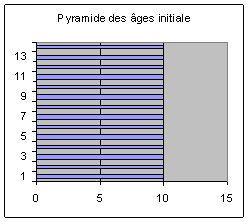
La population totale est donc de 140 millions d’individus ; le taux de croissance est nul ; la population active est de 80 millions de personnes, soit un taux d’activité de 57 %. Le ratio vieux / jeunes, égal au rapport des classes d’âge « plus de soixante ans / moins de vingt ans » est de 50 %. L’âge moyen est de 35 ans.

Nous allons considérer l’évolution de cette population lorsqu’elle subit des chocs de nature diverse.

Variante 1 : Allongement de la durée de vie

Nous supposons que la durée de vie des personnes nées à partir de la date - 50  passe de 70 à 90 ans (on peut supposer par exemple que des médicaments puissants ont été découverts en - 50). Au lieu de mourir à la date 20, ces personnes continuent à vivre. Le cylindre de la pyramide des âges s’allonge et pendant 20 ans de nouvelles classes d’âge s’y ajoutent, jusqu’à ce que la pyramide ait atteint la forme d’un cylindre comportant les classes d’âge jusqu’à 90 ans. Après quoi sa transformation s’arrête.

Voici la comparaison entre les deux régimes stationnaires :

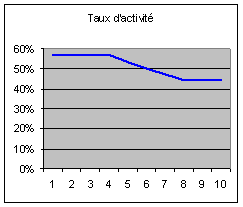
La population totale s’est accrue de 40 millions d’individus ; la population active est restée la même. Le taux d’activité a baissé de 13 points, le rapport vieux / jeunes s’est accru de 100 points, l’âge moyen a crû de 10 ans.

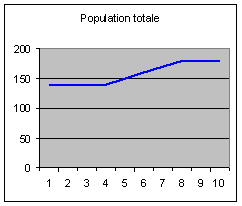
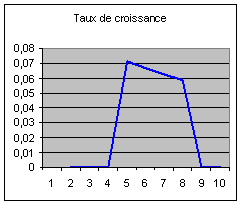
Décrivons la dynamique du passage entre ces deux états stationnaires :

NB : l’axe horizontal dénombre les quinquennats. « 10 » signifie donc « 50 ans ».

Variante 2 : Baisse de la fécondité

Supposons que la fécondité soit divisée par deux à partir de l’année 10. La population considérée ne se reproduit plus à l’identique.

Nous prenons une échelle du temps étendue, de 0 à 280 ans (0 à 56 quinquennats) pour faire apparaître l’issue d’une telle baisse.

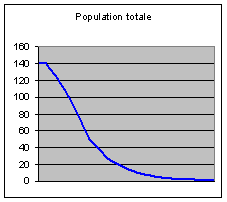
L ‘effectif de la population totale suit une évolution exponentielle décroissante qui la mène vers l’extinction. On ne peut donc pas caractériser de régime stationnaire tendanciel en termes d’effectifs, mais seulement en termes de structure :

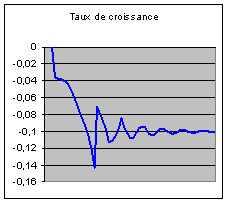
Le taux de croissance quinquennal converge vers –10 %. Cette évolution passe par des oscillations, en raison des fluctuations de la proportion des classes d'âge fécondes dans la population totale. Lorsque la fécondité est divisée par deux, la première génération d’enfants de 0 à 5 ans est de 5 millions au lieu de 10 millions. La population décroît donc de 5 / 140 = 3,6 %. Au quinquennat suivant, la baisse est un peu plus forte puisqu’il s’agit de 5 / 135 = 3,7 %. Ainsi de suite pendant quatre quinquennats. Au bout de 20 ans, la première génération d’effectif faible arrive à l’âge de la fécondité, et la baisse s’accélère.

Au bout de 80 ans, la population a diminué de 64 % (son effectif est de 50 millions) et la pyramide des âges a le dessin suivant :

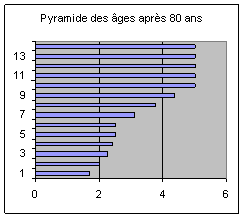
La population d’âge âgé est d’un poids relatif élevé, les classes fécondes sont relativement peu nombreuses, la baisse quinquennale de la population sera alors très rapide (14 %). Dès l’année suivante, le poids des classes d’âge relativement nombreuses diminue et la population ne diminuera que de 7 %.

Au bout de 280 ans, la population ne compte plus que 457 000 personnes. La forme initiale de la pyramide des âges a été effacée et elle a pris la forme suivante, qui sera désormais stationnaire :

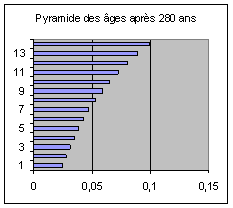
La décroissance de la population se fait dès lors régulièrement au taux de 10 %.

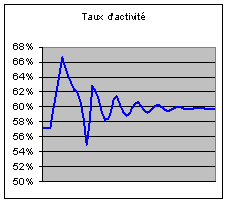
Le taux d’activité connaît des oscillations dont l’explication est analogue à celle que nous avons donnée ci-dessus. Il converge vers 60 % alors que dans la population initiale il était de 57 % :

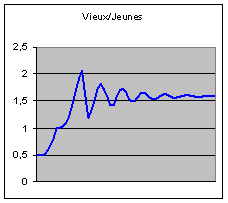
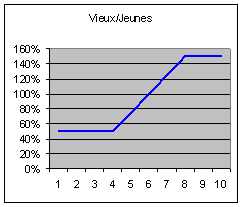
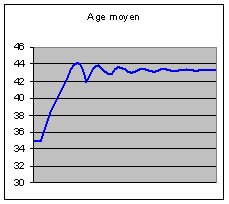
Le rapport des effectifs « vieux / jeunes », égal au départ à 50 %, converge à terme vers 160 %. L’âge moyen converge vers 43 ans alors qu’il était de 35 ans :

Variante 3 : « Baby-Boom »

Nous allons tenter de reproduire ici ce qui s’est passé en France après la seconde guerre mondiale. Pendant la guerre la natalité a été basse en raison de la dureté des temps, et aussi parce que des millions d’hommes étaient prisonniers. Après la Libération,  il y a eu un rattrapage. Sans doute d’ailleurs le phénomène a-t-il été accentué encore par l’arrivée à l’âge fécond des générations relativement nombreuses nées après la guerre de 14-18.

Nous simulerons ce phénomène en supposant que la fécondité, partant du niveau qui assure la reproduction de la population, a été divisée par deux pendant deux quinquennats, puis multipliée par deux pendant les deux quinquennats suivants, et enfin qu’elle est revenue à son niveau antérieur.

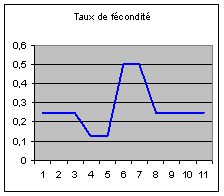
Les graphiques que nous allons produire montrent l’évolution à très long terme suite à un tel choc, car il entraîne des oscillations qui se prolongent pendant longtemps.

Les régimes stationnaires sont très semblables, la seule différence résidant dans la taille de la population, qui passe de 140 à 162. Le taux d’activité est le même.

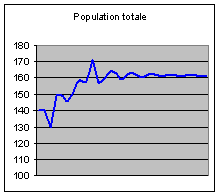
La population totale commence par diminuer (c’est normal, puisque la fécondité commence par baisser), puis elle augmente avec des oscillations, culmine à 170  millions, puis revient avec des oscillations vers 162 millions.

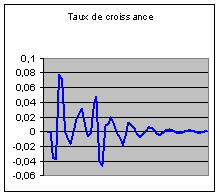
Le taux de croissance subit de fortes oscillations, et en outre celles-ci sont inégales. Après avoir été négatif au début en raison de la baisse initiale de la fécondité, il est évidemment très élevé lors du « Baby-Boom », après quoi il redevient pratiquement nul. Il connaîtra ensuite des fluctuations reflétant le poids relatif des classes d’âge fécondes, qui va osciller par la suite. Le taux d’activité, le rapport vieux / jeunes, l’âge moyen subissent eux aussi de fortes oscillations.

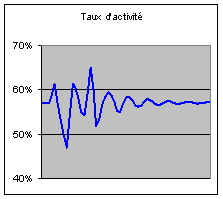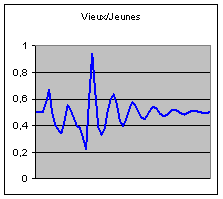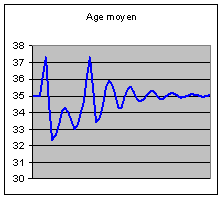
Représentation stylisée de l'histoire démographique

Considérons une population qui, en 1920, serait la population fictive stationnaire de référence, avec un effectif de 40 millions ; infligeons lui la conjonction des deux chocs du vieillissement et du Baby-Boom décrits ci-dessus, puis examinons la dynamique qui en résulte.  

La pyramide des âges de la population française en 1920 n’était pas cylindrique. Cette simulation ne prétend donc pas être réaliste. Elle apporte néanmoins quelques enseignements.

Vieillissement : nous supposerons que le « vieillissement » commence en 1920, c’est-à-dire que les personnes nées cette année là ont une durée de vie de 90 ans, alors que celles nées auparavant ne vivaient que 70 ans. Cette convention schématise un allongement de la durée de vie procuré par un progrès soudain en médecine ou en hygiène semblable à celui qu’ont apporté l’invention des antibiotiques en 1928 (quasi suppression des décès dus aux maladies infectieuses à partir de 1945) et l’amélioration des conditions générales d’alimentation et d’hygiène. Nous choisissons ici de supposer que la première génération à bénéficier de ces progrès est celle née après 1920, presque immédiatement après la première guerre mondiale.

Baby-Boom : nous supposons qu’il y a eu d’abord un « Baby-Crash » (division par deux de la fécondité pendant dix ans, de 1935 à 1945), puis un doublement de la fécondité pendant dix ans également. Ces dates et ces durées ne sont pas exactement réalistes et le « Baby-Crash » de l’occupation n’a évidemment pas débuté en 1935. Cependant la fécondité était notoirement basse avant la deuxième guerre mondiale, et le Baby-Boom a compensé à la fois cette période là et celle de l’occupation. Enfin, l’hypothèse d’une division de la fécondité par deux (par rapport au taux de renouvellement), puis d’une multiplication par deux, serait à moduler si l’on cherchait à être réaliste.

Nous représentons ici les évolutions de 1920 à 2040.

L’évolution de la population totale et de la population active est donnée par le graphique ci-dessous :

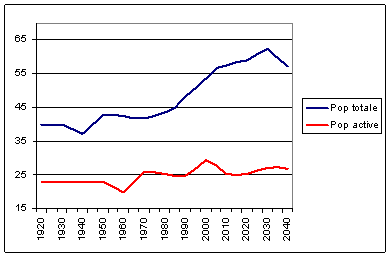
La population active subit des fluctuations résultant d’abord du Baby-Crash, puis du Baby-Boom. La baisse de la fécondité en 1935 entraîne en 1955, vingt ans après, une baisse de la population active qui dure dix ans. Puis à partir de 1965 se fait sentir, pendant dix ans, l’effet du Baby-Boom.

A partir de 1980 la population active décroît un peu pendant dix ans, la classe creuse des enfants des personnes nées pendant le Baby-Crash arrivant à l’âge actif. Puis à partir de 1995 la population active croît fortement pendant dix ans, en raison de l’arrivée à l’âge actif des enfants de la génération du Baby-Boom. La population active décroît pendant dix ans à partir de 2005, en raison du départ en retraite des personnes de la génération du Baby-Boom. Après 2000, les fluctuations se poursuivent en s’amortissant progressivement :   

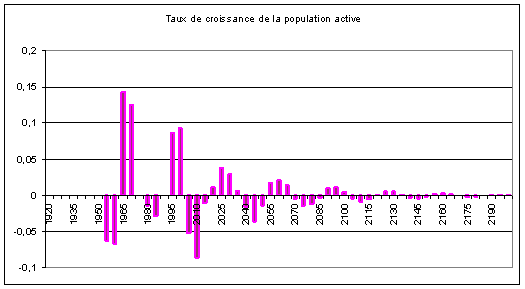
Il en résulte une évolution à long terme de la population active ayant l’allure suivante :

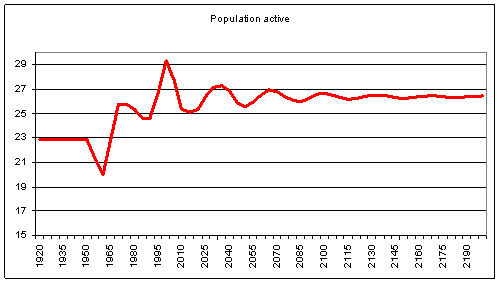
L’effet combiné du Baby-Boom et du Baby-Crash sur la population active est donc à long terme une croissance, puisqu’elle passe de 23 à 26 millions ; le minimum de la population active est de 20 millions en 1960, le maximum est de 29 millions en 2000. Le minimum relatif après 2000 est atteint en 2015 avec 25 millions.

L’évolution de la population totale est plus compliquée que celle de la population active, puisqu’elle est influencée à la fois par les fluctuations de la fécondité et l’allongement de la durée de vie.

La population totale diminue pendant le Baby-Crash de 1935-1945, et croît pendant le Baby-Boom de 1945-1955 qui fait plus que compenser le Baby-Crash. Sur longue période, les fluctuations de la croissance de la population totale se poursuivent après 2000, comme celles de la population active :

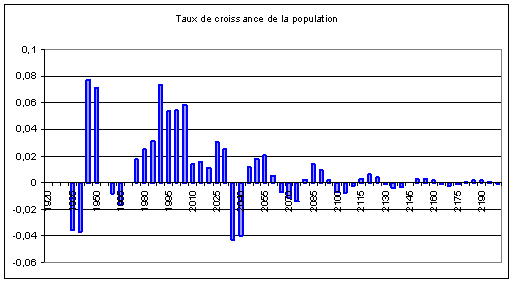
Si l’on regarde l’évolution à long terme de la population totale, on voit que l’effet le plus important est celui du vieillissement ; à long terme la population totale a crû, son effectif se stabilise à près de 60 millions.

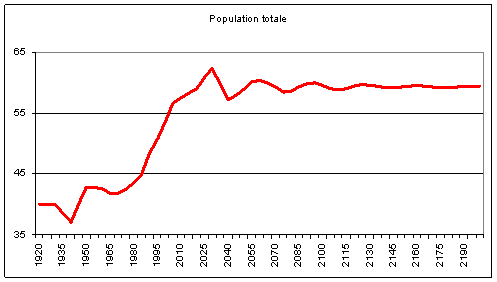
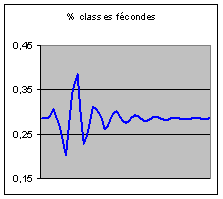
Par convention, la population active est la population de 20 à 60 ans, et les classes fécondes sont les classes de 20 à 40 ans. Il est donc normal que nous trouvions que leurs évolutions ont la même allure. Voici leur pourcentage par rapport à la population totale :

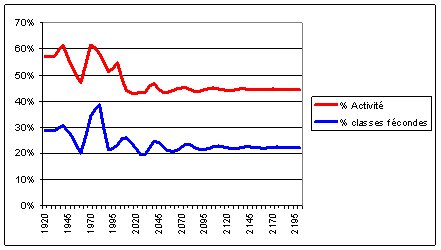
Le taux d’activité, qui est de 57 % au début, décroît pour atteindre 44 % en régime stationnaire. Sa dynamique comporte de fortes oscillations lorsque les effets des chocs se font sentir. S’il n’y avait pas eu le vieillissement, le taux d’activité aurait connu un pic de 65 % en 2000 ; au lieu de quoi il ne fait à cette date qu’une timide remontée vers 55 %. 

Au moment du Baby-Crash, le taux d’activité augmente puisqu’il y a moins de jeunes inactifs. Puis il diminue au moment du Baby-Boom, et atteint un minimum de 47 % en 1960. Il remonte ensuite et atteint un maximum de 62 % en 1970. Le passage des classes nombreuses du Baby-Boom à l’âge actif le maintient à un niveau relativement élevé pendant les années 95 et 2000, puis l’effet du vieillissement l’emporte et il reste durablement bas avec quelques fluctuations.

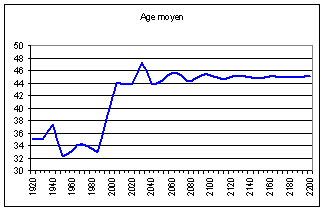
L’âge moyen, qui était de 35 ans avant les chocs, devient à long terme de 45 ans. L’effet du vieillissement est prépondérant sur cette variable ainsi que sur le rapport entre jeunes et vieux.

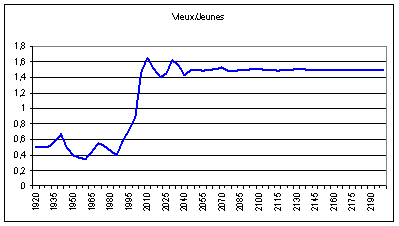
Les inflexions de la fécondité ne font qu’apporter des fluctuations relativement négligeables par rapport à l’effet principal.

Conclusion

Le Baby-Crash et le Baby-Boom apportent de la volatilité aux évolutions de la population totale et du taux d’activité, mais la tendance essentielle est celle donnée par le vieillissement.

Les oscillations provoquées par la succession du Baby-Crash et du Baby-Boom se font sentir jusqu’au milieu du XXI^e siècle et compliquent notablement le dimensionnement des ressources nécessaires à certaines classes d’âge, notamment celles du système éducatif et du système de santé.

Si l’on observe plus précisément l’évolution de la population totale à la fin du XX^e siècle, on voit que la hausse provoquée par les suites du Baby-Boom dans les années 80 est relayée par le vieillissement dans les années 90.

Les oscillations que nous avons constatées sont d’un grand intérêt. Elles montrent qu’après un choc ponctuel les données statistiques peuvent évoluer dans un sens contraire à la tendance résultant du choc sans que cela remette en question la logique qui détermine fondamentalement leur évolution. Il est donc nécessaire, lorsque l’on interprète des fluctuations, de disposer  d’un modèle permettant de les rapporter à leur cause : sans un tel modèle, on risque d'être tenté de les expliquer par une conjoncture qui, en fait,  n’existe pas.