Choisir la date du lancement d'un projet

19 janvier 2002

Le coût du capital diminue avec les nouvelles technologies : on observe une baisse de coût de 30 % par an pour les équipements et de 4 % par an pour la production des logiciels. Il en résulte une évolution de la rentabilité des projets : tel projet non rentable l’année A₁ sera rentable l’année A₂ parce que le coût de l’investissement aura diminué. Ainsi la question n'est pas de savoir si le projet est rentable ou non dans l'absolu (il deviendra rentable un jour en raison de la baisse continue du coût), mais de savoir à quelle date il convient de le lancer. On peut poser la question autrement : au lieu de chercher à déterminer une date, on peut chercher à préciser selon quelles données observées aujourd'hui on peut prendre la décision de lancer ou non le projet. 

Le raisonnement est souvent le suivant : le projet est rentable aux conditions d'aujourd'hui ; mais il le sera davantage aux conditions de l'année prochaine, en raison de la baisse du coût ; cependant si l'on attend on perd un an du bénéfice que le projet apporterait. Comment arbitrer entre ces diverses considérations ? Le raisonnement devient encore plus compliqué quand l'entreprise prend en considération la prime au premier entrant sur un nouveau marché (si elle attend pour lancer le projet, la recette qu'elle peut anticiper est plus basse). 

Le modèle ci-dessous a pour but d’éclairer les intuitions qui guident la décision dans de telles circonstances. Nous construirons d'abord un modèle simple prenant en compte la baisse du coût des équipements ; puis nous l'enrichirons pour introduire la baisse de l'anticipation de recette. 

Effet de la baisse du coût des équipements

Considérons un projet nécessitant un investissement de coût p et rapportant par la suite le résultat annuel R pendant une durée infinie. La valeur actuelle nette (VAN) de ce projet selon le taux d’actualisation τ[1] et son taux de rentabilité interne (TRI) sont :

(1) VAN = - p + R ∫e^-τtdt = R/τ - p

(2) TRI = R/p,

Notons avec l'indice "a" la date d'aujourd'hui. Supposons que le coût d’investissement diminue selon la loi :

(3) p_t = p_ae^{-δ(t - a)}

Si l’investissement est réalisé à la date t, la VAN du projet à cette date sera donc :

(4) V_t = R/τ – p_t

Cette VAN rapportée à la date a (et non au début du projet) sera, en supposant a = 0 pour simplifier les notations :

(5) W_a = V_te^-τt = [R/τ - p_ae^-δt]e^-τt

Si l’on retarde un investissement deux effets de sens contraire jouent : d’une part V_t croît parce que le coût de l’équipement diminue ; d’autre part W_a diminue en raison du facteur d’actualisation e^-τt.

Le calcul indique que la date optimale pour l’investissement (celle qui maximise W_a) est D telle que :

(6) D = a + (1/δ) Log [p_a(δ + τ)/ R]

Prenons pour valeurs numériques p_a = 200, R_a = 25, τ = 15 %, δ = 30 %.

L’évolution de W_a en fonction de t a l’allure suivante :

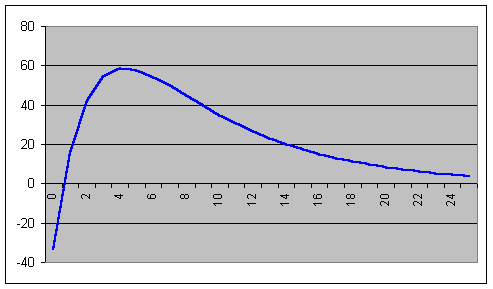
Si l’investissement était réalisé à la date a, la VAN V_a serait négative (en effet, la rentabilité du capital serait alors de 25/200 = 12,5 %, donc inférieure au taux d’actualisation). La VAN devient nulle si l’on attend un an pour investir. W_a est maximale si l’on réalise le projet à l’année 4 (le calcul donne exactement D = 4,27 ; alors W_a = 58,56).

Si l’on avait fait le calcul à partir de l’année a + 1 et non de l’année a, il aurait fallu prendre pour coût du capital p_{a + 1} = 200*e^-τ = 172,14. La valeur actuelle nette W_{a + 1} (évaluée à la date a + 1) d’un projet réalisé l’année t est alors :

(7) W_{a + 1} = V_te^{-τ(t - 1)} = e^τW_a

La date D qui permet de maximiser W_a est aussi celle qui permet de maximiser W_{a + 1}. La date à laquelle le projet doit être réalisé est donc indépendante de la date à partir de laquelle on fait le calcul.

Il est intéressant de considérer le cas particulier où D = a : dans ce cas, il faudrait réaliser l’investissement immédiatement. D’après (6), on a alors :

(8) TRI₁ = R_a/p_a = δ + τ

Sous les hypothèses que nous avons retenues, la date optimale serait donc celle où le TRI devient égal au taux d’actualisation augmenté du taux de baisse du coût de l’investissement. Ainsi, dans le cas que nous avons considéré où τ = 15 %, δ = 30 %, l’investissement doit être réalisé à la date où le TRI est de 45 %.

Si p_a est tel que :

(9) R_a/p_a ≥ δ + τ, on a D ≤ a.

Si l’inégalité est stricte, l’entreprise a laissé passer la date où la valeur du projet aurait été maximale, et il faut donc qu’elle le réalise immédiatement.

Ainsi se trouve modélisé le raisonnement qui consiste à attendre que le coût des équipements ait baissé assez pour rendre l’investissement profitable. L’entreprise ne doit pas investir dès que le projet devient rentable (R_a/p_a = τ), ni non plus attendre indéfiniment que la rentabilité croisse (puisque R/p tend vers l’infini lorsque p tend vers zéro), mais elle doit attendre que p ait suffisamment diminué pour que (9) soit vérifiée.  

Alors que la relation (6) permet à l'entreprise de savoir à quelle date dans le futur il faudra investir, la relation (9) lui permet de décider s'il faut investir maintenant ou non. Elle répond donc à un autre type de question. La direction de la stratégie, ainsi que la direction du marketing, peuvent être intéressées par la connaissance de la date future de l'investissement ; mais la direction de la production, la direction informatique, qui ont un horizon plus court, s'intéressent surtout à la construction du programme d'investissement de l'année courante et la relation (9) répond à ce besoin. 

Pour pouvoir appliquer la relation (9), il faut que l'entreprise connaisse le prix p_a du bien d'équipement aujourd'hui, la recette anticipée R_a et le taux d'actualisation τ : ce sont là des informations que doit avoir quiconque veut évaluer un projet ; mais il faut en outre qu'elle connaisse le taux δ de baisse du coût du capital. Cette dernière information s'obtient en observant l'évolution passée de ce coût et en inférant ce que sera son évolution future.  

Variante sur la baisse du coût du capital

Supposons que δ = 10 % (courbe rouge ci-dessous ; la baisse du coût du capital est plus lente que dans le cas considéré précédemment) :

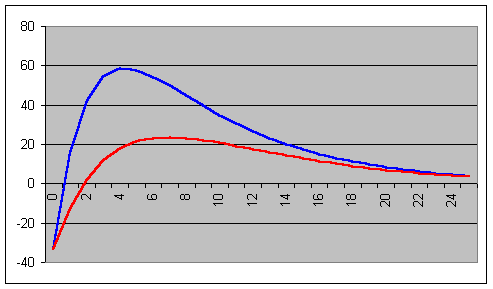
On trouve dans ce cas que la VAN est plus basse et que la date optimale d’investissement est plus tardive (le calcul donne D = 6,93 ; alors W_a = 23,57).

Effet d'une baisse de la recette anticipée

On peut enrichir le raisonnement en introduisant une autre considération : l’entreprise qui investit la première peut espérer un résultat plus élevé que celles qui viendront plus tard, que ce soit en raison de la prime au premier entrant sur le marché d’un nouveau produit ou du gain de compétitivité apporté par une nouvelle technique de production. On peut aussi supposer que le résultat annuel sur le marché considéré décroît exponentiellement dans le temps en raison de l'arrivée progressive de nouveaux concurrents. Résumons ces hypothèses en supposant que la recette annuelle anticipée dépend de la date t de l’investissement selon la relation :

(10) R_t = R_ae^{-μ(t  - a)}

On trouve alors, en supposant a = 0 pour simplifier les notations :

(11) W_a = [(R_ae^-μt )/τ - p_ae^-δt]e^-τt

Et la date optimale pour l’investissement est alors :

(12) D = a + [1/ (δ – μ)] Log [τp_a(δ + τ) / R_a(μ + τ)]

Reprenons le raisonnement qui a conduit à la relation (8) : il faut réaliser l’investissement immédiatement si p_a est tel que le TRI soit :

(13) TRI₂ = R/p = τ(δ + τ)/(μ + τ)

Supposons que où τ = 15 %, δ = 30 % comme ci-dessus, et qu’en outre µ = 10 % ; on trouve alors que TRI₂ = 27 %.

Ainsi, si l’entreprise tient compte de la baisse tendancielle de la recette anticipée, son exigence de rentabilité est plus faible que si la recette anticipée était indépendante de la date du projet.  Si µ < δ (c’est-à-dire si la baisse de la recette anticipée est moins rapide que la baisse du coût de l’investissement), le taux de rentabilité à exiger reste supérieur au taux d’actualisation. Si µ > δ, l’investissement doit être réalisé immédiatement (V_t ne fera que décroître par la suite) à condition toutefois que R_a/p_a > τ.

Variante sur la baisse de la recette anticipée

Supposons que μ = 10 % (cela donne la courbe rouge ci-dessous).

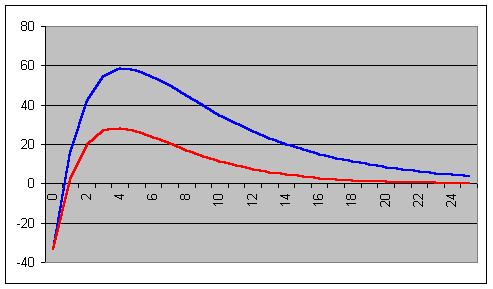
La VAN du projet est plus basse, mais la date à laquelle il convient de réaliser l’investissement est plus précoce (le calcul donne D = 3,85 ; alors W_a = 28,29).

Conclusion

Cet exercice a fourni un résultat conforme à l’intuition : si le coût du capital diminue, un projet non rentable à une date donnée peut devenir rentable par la suite ; il en résulte que les entreprises doivent mettre à jour les évaluations de rentabilité des projets (et non associer définitivement à un projet donné une image de non rentabilité).

On trouve aussi un résultat moins intuitif : si le coût du capital baisse indéfiniment, certes la VAN calculée à la date de l’investissement croît indéfiniment, mais il existe une date à partir de laquelle il convient de ne pas retarder l’investissement. Le taux de rentabilité à retenir alors est toutefois nettement plus élevé que le taux d’actualisation.

Enfin, retarder un projet peut avoir pour conséquence non seulement de diminuer son coût, mais aussi de diminuer la recette que l’on peut en attendre ; si elle prend en compte ce dernier phénomène, l’entreprise sera conduite à investir de façon plus précoce et à exiger une rentabilité moindre.