|
Effet des règles de gestion
du budget informatique
24 mai 2001
Les directions générales
cherchent à maîtriser le " centre de coûts " informatique
en se donnant des règles simples. Ces règles ont fait l’objet d’une étude
systématique (Peter G. W. Keen, Shaping the Future, Business Design through
information technology, Harvard Business School Press 1993).
Le modèle de Keen tient compte
des paramètres suivants :
- obsolescence des logiciels (durée de vie),
- baisse tendancielle du coût des unités
d ’œuvre,
- stock
des logiciels en exploitation, flux des développements, coût de
maintenance et d’exploitation.
L’économie du SI apparaît
alors comme celle d’une ressource en capital que l’on
stocke, entretient et renouvelle. Cette approche ne considère pas les autres aspects de l’économie du SI, mais
elle permet de mettre en évidence les effets pervers des règles simples :
explosion ou implosion non maîtrisées des dépenses, écrasement de la part
des nouveaux développements.
Voici les évolutions du budget
informatique selon les règles retenues, en supposant que la durée de vie est
de cinq ans et que le prix des unités d’œuvre diminue de 20 % par an ;
elles comportent toutes un caractère exponentiel, c’est-à-dire qu’elles
sont difficiles à maîtriser. Si le stock des applications est
constant en volume, le budget des études s’aligne de façon à assurer le renouvellement du stock en compensant l’obsolescence. La
baisse du coût des unités d’œuvre se reflète par une
diminution exponentielle du budget informatique :
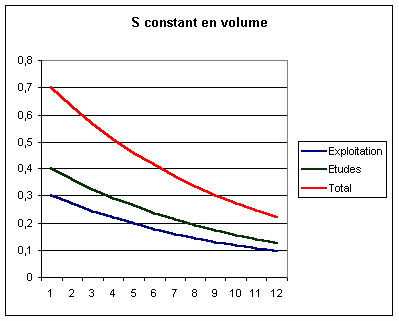
Stock constant d’applications
informatiques
Si le flux des nouveaux
développements est constant, cela se traduit d’abord par une augmentation du
stock des applications en exploitation (si l’on suppose que l’on part de
zéro), puis par une stabilisation de ce stock, les nouveaux développements
étant compensés par l’obsolescence ; on se retrouve alors dans une
situation analogue à celle de la simulation précédente :
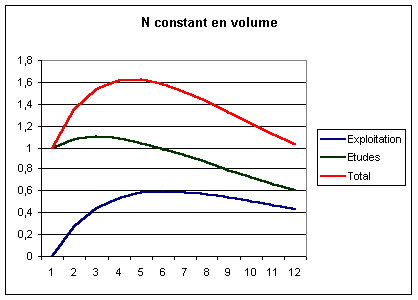
Flux constant des nouveaux
développements
Si le coût des nouveaux
développements est constant, on obtient à terme un budget informatique
constant. Cette politique a donc un effet stabilisateur sur le coût de l’informatique
:
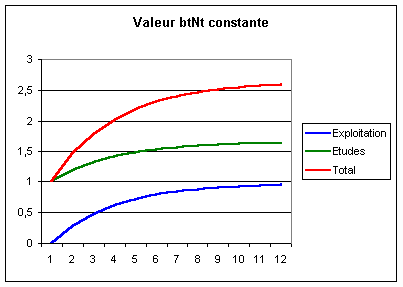
Coût constant des nouveaux
développements
Si la part des nouveaux
développements dans le budget informatique est constante, il en résulte une
évolution exponentielle du budget : elle est croissante si les nouveaux
développements font plus que compenser l’obsolescence et la diminution du
coût des unités d’œuvre, décroissante dans le cas contraire :
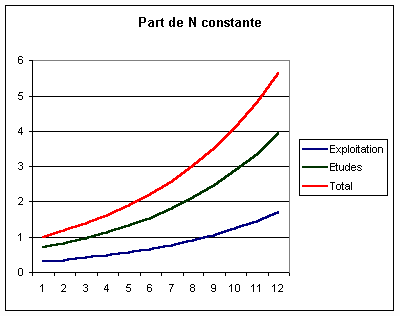
Part constante des nouveaux
développements
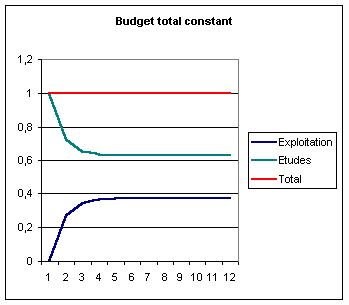
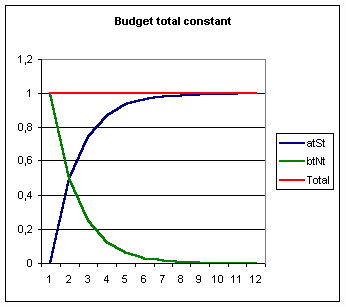
La règle " budget
informatique constant " conduit, si l’obsolescence est faible et la
baisse de prix négligeable, à annuler les dépenses consacrées à l’innovation :
la totalité du budget informatique sera consacrée à la maintenance et l’exploitation
du stock existant. Cet exemple assez saisissant montre les conséquences
extrêmes que peut avoir une règle de gestion simple et (apparemment) de bon
sens.
On peut enfin tenter de définir le
degré optimal d'informatisation d'une entreprise. En utilisant les méthodes de
l'optimisation dynamique, on trouve que si le coût des unités d'œuvre
n'évolue pas le taux d'informatisation optimal est donné sous certaines
hypothèses par la relation ci-dessous :
s* = {[a + b(r + d)]/µ}1/(m
- 1)
où s est le taux d'informatisation
par tête, a le coût unitaire d'exploitation de l'informatique, b le coût
unitaire d'investissement en informatique, r le taux d'actualisation, d
le taux d'obsolescence, µ l'exposant du facteur de production
"informatique" dans une fonction de production de Cobb-Douglas (je
tiens la démonstration à la disposition des personnes intéressées).
Je n'ai pas encore trouvé
l'expression de s* lorsque le coût unitaire décroît ; les simulations
numériques indiquent que dans ce cas, à l'optimum, le rapport entre budget
informatique et valeur de la production de l'entreprise reste constant. Comme la
baisse du coût de l'informatique permet d'accroître cette valeur, il en
résulte qu'en cas de baisse du coût unitaire le budget informatique optimal
doit croître. Ce n'était pas évident a priori ; en fait je m'attendais au
résultat contraire.
|