|
Modèle marketing des services documentaires payants
5 février 2000
L'objet de cette fiche est de fournir les éléments
essentiels pour comprendre et modéliser les aspects marketing d'un nouveau service
documentaire payant sur le Web.
Elle ne traite pas les composantes
" gratuites " de tels services (sponsoring, affichage publicitaire,
fonction de portail) : ces composantes sont caractéristiques du marketing du Web, et
donc importantes, mais leur logique n’est pas celle du contenu payant à laquelle
nous nous limitons ici.
Les déterminants de la diffusion du service (rapport qualité /
prix, préférences des clients, rythme de pénétration) sont examinés sous une forme
simplifiée permettant un traitement numérique complet en vue de comparer des stratégies
d'offre.
Introduction
Nous commencerons par spécifier la fonction d'utilité
du client d'un tel service ; nous présenterons ensuite un modèle décrivant les
mécanismes de diffusion d'un service en fonction de ses caractéristiques de
qualité et de prix. Ce modèle sera complété dans deux directions : (1) nous
explorerons le cas particulier de la diffusion lorsque le service est différencié en gamme
; (2) nous décrirons les propriétés de formules tarifaires plus complexes que
celle retenue initialement.
Enfin, nous montrerons comment ce modèle marketing peut être
inséré dans un modèle économique susceptible d'éclairer la prise de décision
d'un offreur de services, et évoquerons les problèmes posés par les estimations
économétriques nécessaires pour donner au modèle un contenu quantitatif et une
portée opérationnelle.
Fonction d'utilité
Il faut mettre en évidence les propriétés les plus
importantes de la fonction d’utilité pour la question que nous étudions. Nous
retiendrons ici une spécification simple et ferons l'impasse sur certains phénomènes
comme la substitution du service avec d'autres services existants.
Un service documentaire apporte au client une utilité
dépendant :
- de la qualité du stock de documents ;
- du nombre de documents disponibles ;
- de la commodité de l'accès au stock.
Le dernier paramètre dépend des outils utilisés et de la
qualité de l'indexation. Le premier paramètre dépend de la pertinence de la politique
éditoriale qui a présidé à la constitution du stock .
Toutes choses égales d'ailleurs, pour une qualité éditoriale
et technique donnée, l'utilité du service est fonction croissante du nombre de documents
: plus ce nombre est élevé, plus la probabilité que le document désiré par le client
soit présent dans le stock est forte.
La fonction d'utilité du service dépend aussi des offres
concurrentes : l'utilité est plus faible s'il existe déjà un service analogue. Nous
montrerons dans la partie consacrée à la différenciation comment l'offre d'un service
voisin peut affecter la demande.
Nous n'examinons pas ici l'équilibre du marché de l'ensemble
des services Web, mais celui d'un service considéré isolément. L'étude du marché de
l'ensemble des services nécessiterait de formaliser l'équilibre de concurrence
monopoliste qui résulte à terme des comportements d'offre de nouveaux services. Comme
les services Web sont encore relativement récents, on est loin de ce point d'équilibre ;
la différenciation des services étant réduite, on peut supposer que chacun est en
position de monopole de facto dans la " niche " pour laquelle
il a été construit. C'est cette situation que nous allons décrire.
Chaque offreur doit cependant avoir présente à l'esprit la
perspective d'un renforcement de la concurrence et doit s'y préparer en établissant
l'équilibre économique de son offre sur une période courte (de l'ordre de cinq ans au
plus), et en lui conférant le niveau de qualité et de prix qui l'aidera par la suite à
résister à l'émergence d'offres voisines.
Nous caractériserons chaque client par le paramètre
l définissant sa fonction d'utilité :
(1) u l = U(N) - l.p,
où N est le nombre de documents fournis par le service et
où N est le nombre de documents fournis par le service et
l représente la sensibilité du client l au prix du service : plus l est grand, plus la décision du client est
influencée par le prix. U(N) est telle que U' > 0 et U" < 0 (cela signifie que
l'utilité marginale d'un document supplémentaire, toujours positive, est d'autant plus
faible que N est plus grand).
Si l = 0,
le client n'est sensible qu'à U(N).
Si l >
0, ul devient
négatif lorsque p > U(N)/l : dans
ce cas, le client n'achète pas le service.
Dans le plan (N, p), la courbe d'indifférence correspondant à
des valeurs données de l et de u a
pour équation :
(2) p = [U(N) - u]/ l
Supposons U(N) de la forme k.ln(N/N0)
où ln est le logarithme népérien.
Considérons les courbes d'indifférence pour une même valeur
de l et des valeurs
différentes de l'utilité (il s'agit donc des courbes d'indifférence d'un même client)
; elles sont parallèles :

Graphique 1 : courbes d'indifférence d'un client
Considérons maintenant les courbes d'indifférence pour une
même utilité et des valeurs diverses de l (il s’agit de courbes d'indifférence correspondant à un même niveau
d'utilité pour des clients différents) ; elles sont affines les unes des autres et
coupent toutes l'axe des abscisses au point tel que u = U(N).

Graphique 2 : courbes d'indifférence de divers clients pour une même
utilité
En partant de ces deux graphiques, on se représente l'ensemble
des courbes d'indifférence, que l'on considère un client ou des clients différents.
Modèle de diffusion
Précisons le vocabulaire utilisé :
- " clientèle potentielle " : clientèle du service à
terme, lorsque son niveau asymptotique a été atteint.
- " pénétration " : fonction du temps déterminant la
façon dont l’effectif de la clientèle rejoint celui de la clientèle
potentielle.
- " diffusion " : variation de l’effectif de la
clientèle, résultant d’éventuelles évolutions de la clientèle potentielle (si le
prix ou la qualité changent) ainsi que de la pénétration.
La diffusion d'un nouveau service est ainsi représentée par la
combinaison de deux lois :
- l'une décrit l'évolution de la clientèle potentielle ;
- l'autre décrit la dynamique de pénétration dans la clientèle potentielle.
Clientèle potentielle
La taille de la clientèle potentielle dépend de la qualité du
service et de son prix. l étant
positif, on supposera que la répartition de la population selon le paramètre l suit une loi Log-Normale (i. e. le logarithme de l suit une loi normale). La taille de
la clientèle potentielle s'exprime, à partir de cette loi, en fonction du prix et de la
qualité du service.
La loi Log-Normale a pour densité de probabilité :
(3) f(x) = (1/(x * s * (2p)1/2))*exp((-1/2)*((ln(x) - m)/1/2))*exp((-1/2)*((ln(x) - m)/ s)2)
Elle est déterminée par les deux paramètres m et
s. Ses valeurs caractéristiques sont :
(4) mode : exp (m -
s2)
(5) moyenne : exp (m + s
s2/2)
(6) écart type : exp (m +
s2)*(1 - exp(- s
s2))1/2
Le client l
envisage de s'abonner si u
l
envisage de s'abonner si ul > 0, c'est-à-dire si p < U(N)/l. Si pour une valeur donnée de N on
représente les valeurs de ul en fonction de l, on
trouve le graphique suivant qui met en évidence le seuil de décision:
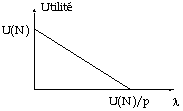
Graphique 3 : seuil de décision
Le seuil de décision dépend donc de N et de p. La clientèle
potentielle va varier en fonction de ces deux paramètres. Si l'on représente l'utilité
en fonction de l et la fréquence des
valeurs de l, on visualise la taille
de la clientèle potentielle : c'est la surface contenue sous la courbe représentative de
la loi Log-Normale et située à gauche de la droite AB. Si p diminue, ou si N augmente,
le point A se déplace vers la droite et la clientèle potentielle augmente.
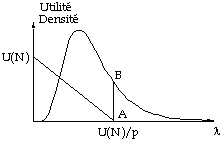
Graphique 4 : seuil de décision et clientèle potentielle
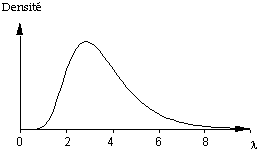
Graphique 5 : distribution de densité selon l
Supposons que la distribution de
l suive la loi Log-Normale de moyenne 3,6 et d'écart-type 1,5 représentée
sur le graphique 5, et que les décisions concernant les paramètres N et p provoquent
l'évolution suivante du rapport U(N)/p (cette évolution par palier se produira par
exemple si N reste constant et que l'on diminue le prix par étapes) :
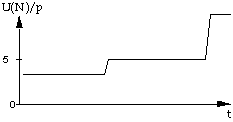
Graphique 6 : évolution de U(N)/p
La population potentiellement intéressée par le service
évolue ainsi :

Graphique 7 : évolution de la clientèle potentielle
Chaque baisse de prix (ou chaque augmentation de la qualité)
élargit donc la clientèle potentielle du service. On observe que la première baisse de
prix fait gagner davantage de marché potentiel que la seconde, bien que celle-ci soit
plus forte : cela résulte de la forme de la distribution de l.
Courbe de demande
On peut à partir des indications précédentes retrouver la
forme classique de la courbe de demande (potentielle) en fonction du prix du service pour
un niveau de qualité donné ; le modèle permet aussi de représenter l'incidence de la
qualité sur la demande pour un niveau de prix donné.
Notons U0 la qualité de
service supposée constante. Le "prix de réservation" p, au dessous duquel le
client
Courbe de demande
On peut à partir des indications précédentes retrouver la
forme classique de la courbe de demande (potentielle) en fonction du prix du service pour
un niveau de qualité donné ; le modèle permet aussi de représenter l'incidence de la
qualité sur la demande pour un niveau de prix donné.
Notons U0 la qualité de
service supposée constante. Le "prix de réservation" p, au dessous duquel le
client l achètera le service, est :
(7) p = U0/l.
Comme
Comme l est
distribué selon la loi Log-Normale (m, s), p est distribué selon la loi Log-Normale (ln(U0)
- m, s).
La courbe de demande est obtenue en utilisant la fonction
cumulative de cette distribution ; elle a la forme suivante :
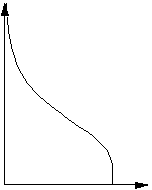
Graphique 8 : courbe de demande
Demande potentielle et qualité du service
Notons p0 le niveau de prix
supposé constant. La "qualité de réservation" N, pour laquelle le client
La courbe de demande est obtenue en utilisant la fonction
cumulative de cette distribution ; elle a la forme suivante :

Graphique 8 : courbe de demande
Demande potentielle et qualité du service
Notons p0 le niveau de prix
supposé constant. La "qualité de réservation" N, pour laquelle le client
l achètera le service, est telle que
(8) U = l.p0, avec U = k.ln(N/N0).
Pour simplifier les notations, nous supposerons ci-dessous que N0 = 1 (ceci revient à supposer que l'on mesure le nombre de
documents en prenant pour unité de volume le nombre N0
de documents tel que U(N0) = 0).
ln(N) suit la loi Log-Normale (m + ln(p0)
- ln(k), 0, avec U = k.ln(N/N0).
Pour simplifier les notations, nous supposerons ci-dessous que N0 = 1 (ceci revient à supposer que l'on mesure le nombre de
documents en prenant pour unité de volume le nombre N0
de documents tel que U(N0) = 0).
ln(N) suit la loi Log-Normale (m + ln(p0)
- ln(k), s). La demande potentielle
en fonction de N a la forme suivante :
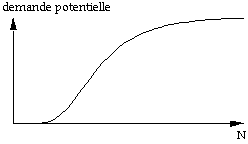
Graphique 9 : demande potentielle en fonction de la qualité du service
Pénétration du service
La pénétration du service en fonction du temps pour une
clientèle potentielle donnée est représentée par une loi de Gompertz (préférable ici
à la loi logistique qui a l'inconvénient de placer l'origine du temps à - ¥ ) :
(9) y =

Graphique 9 : demande potentielle en fonction de la qualité du service
Pénétration du service
La pénétration du service en fonction du temps pour une
clientèle potentielle donnée est représentée par une loi de Gompertz (préférable ici
à la loi logistique qui a l'inconvénient de placer l'origine du temps à - ¥ ) :
(9) y = a .
exp [- exp (g (t0 - t)) ]
Lorsque t -> ¥ , y
-> 0 - t)) ]
Lorsque t -> ¥ , y
-> a ; le coefficient a représente donc la taille de la clientèle
potentielle. Plus g est élevé, plus
la convergence est rapide. t0 est l'abscisse du point
d'inflexion de la courbe ; lorsque t = t0, le taux de
pénétration est de 36,79 %. Nous poserons b = g t0 et utiliserons la notation :
(10) y = 0 et utiliserons la notation :
(10) y = a
. exp [- exp (b - g . t) ]
Pour un service Web,
Pour un service Web,
g est élevé en raison de l'effet d'avalanche résultant des comportements
d’imitation, et b est élevé en
raison de la lenteur de la pénétration initiale. Ces deux coefficients dépendent par
ailleurs de la qualité de la politique commerciale et de la politique de communication
menée par l'offreur.
La forme de la loi de Gompertz est donnée par le graphe
ci-dessous :
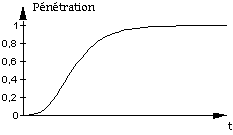
Graphique 10 : loi de Gompertz
Diffusion du service
Le mécanisme d'ensemble de diffusion d'un nouveau service
comporte trois étapes :
- évolution du paramètre critique, fonction du prix et de la
qualité de service, déterminant les seuils d'acceptation pour les clients potentiels ;
- taille de la clientèle potentielle, en fonction de la
position du paramètre ci-dessus par rapport à la distribution de la sensibilité au prix
l dans la population ;
- rythme de pénétration dans la clientèle potentielle.
Lorsque l'on passe d'une phase de diffusion à la suivante (par
exemple à l'occasion d'une baisse de prix), on passe sur une nouvelle loi de Gompertz.
Nous supposons que le coefficient g
de la nouvelle loi est le même que celui de la loi précédente, le coefficient b s'ajustant pour tenir compte de la pénétration
déjà acquise.
La diffusion du service se fait alors selon une succession de
lois de Gompertz, chacune s'enchaînant à la précédente et ayant pour niveau
asymptotique la clientèle potentielle correspondant aux valeurs prises par la qualité et
le prix du service. Si l'on prend pour exemple le cas évoqué ci-dessus, on trouve la
courbe de diffusion suivante :
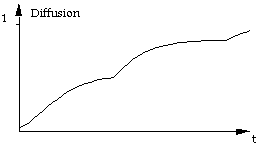
Graphique 11 : diffusion du service
Des politiques de prix plus contrastées peuvent susciter un
profil de diffusion plus accidenté : ainsi, si l'on suppose que le rapport U(N)/p varie
de la façon suivante :
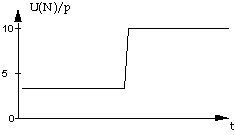
Graphique 12
on obtient le graphe de diffusion suivant :
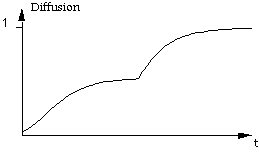
Graphique 13
La baisse de prix (ou la hausse de la qualité) relance donc la
diffusion, alors que celle-ci avait atteint pratiquement toute la clientèle potentielle
concernée par les premières valeurs des paramètres de prix et de qualité.
Stratégie d'offre
Considérons un offreur se trouvant en situation de monopole de
facto, en raison de la nouveauté de l'offre de services Web (lorsque cette offre sera
à maturité, il faudra utiliser un modèle de concurrence monopolistique). Sa stratégie
d'offre va consister à maximiser le profit actualisé compte tenu des informations qu'il
possède sur la demande.
La fonction de coût dépend du nombre N de documents et du
nombre n de clients. Nous la noterons c(N, n). Si on la suppose affine en N et n
séparément, elle a la forme :
(11) cI(N, n) = F + a.N +
b.n + c.N.n pour les dépenses d'investissement (à compléter par l'indication de la
durée de vie des matériels et logiciels),
(12) cE(N, n) =
F + a.N + b.n + c.N.n pour les dépenses d'exploitation.
L'offreur doit choisir parmi les combinaisons (N, p) ; si l'on
note n(N, p) la demande qui répond à une telle offre, et si l’on ne tient pas
compte du temps, l'offreur doit résoudre le programme en (N, p) du type suivant :
(13) max {p.n(N, p) - c(N, n(N, p))}.
Le traitement complet du problème suppose que l'offreur tienne
compte de la loi de pénétration du service ainsi que de l'évolution du coût de
production. Dans le domaine des services Web, la stratégie d'offre sera fonction du temps
: l'offreur doit la déterminer de façon à maximiser la valeur actuelle nette de son
projet, qui peut s'écrire en notant A le taux d'actualisation (A est la somme du taux
d’intérêt d’un placement sans risque sur le marché, et de la prime de risque
jugée raisonnable pour un projet de ce type) :
(14) StÎ [0, ¥ ] [{p(t).n[N(t), p(t)] - c[N(t), n[N(t),
p(t)], t]}/(1 + A)t]
(La somme est prise en fait non sur l’infini, mais sur
l’intervalle de temps représentant la durée de vie plausible du service).
Il serait difficile de résoudre un tel programme sous forme
analytique, même en utilisant comme nous l'avons fait des spécifications fonctionnelles
simples ; cependant il est aisé de le résoudre sous forme numérique en procédant par
simulation.
La stratégie d'offre répondant à une évolution donnée des
coûts de production comportera donc d'une part une chronique N(t) représentant la
qualité du service offert, d'autre part une chronique de prix p(t). L'offre d'un service
documentaire sur le Web sera donc évolutive, même si l’on ne tient pas compte des
conditions de concurrence propres à ce marché. Il est d'autant plus nécessaire
d'organiser cette évolution dès la conception même du service.
Différenciation du service
Nous avons jusqu'à présent supposé que le service était
offert sous une seule forme. Il est souvent intéressant, pour toucher divers segments de
clientèle, de différencier en " gamme " l'offre de services; la
différenciation peut porter soit sur le contenu de la base documentaire (plus ou moins
riche), soit sur le mode d'accès (plus ou moins confortable), soit sur les deux
caractéristiques. Le service de qualité moindre sera vendu à un prix plus bas.
Nous décrirons d'abord comment formaliser l'offre en gamme,
puis lui appliquerons le modèle précédent afin de représenter la réaction des clients
à une telle offre. Il en découle des indications relatives aux effets des stratégies
d'offre sur la diffusion d'un service.
Offre d’une gamme
Pour schématiser le cas où le service est offert en gamme,
nous supposerons que deux types d'accès et de stocks sont prévus :
- l'un concernant des documents stockés en mode caractère, et
offrant N1 documents à la consultation ;
- l'autre concernant des documents stockés en mode image (et
comprimés de façon que la durée de transmission soit analogue à celle des documents en
mode caractère), offrant N2 = 10 x N1 documents.
Deux services différents seront offerts :
- un service "bas de gamme" S1,
offrant le premier type d'accès seulement ;
- un service "haut de gamme" S2,
offrant les deux types d'accès.
Nous noterons N2 > N1 le nombre d'ouvrages
accessibles avec S2. U(N) étant fonction croissante
de N, U(N2) > U(N1).
Nous supposerons pour simplifier le raisonnement que ces deux
services sont vendus pour des prix forfaitaires p1 et
p2 avec p2 >
p1 (cette hypothèse sera enrichie par la suite pour
introduire des tarifications plus complexes).
Réaction des clients à une offre en gamme
Le client t]
(La somme est prise en fait non sur l’infini, mais sur
l’intervalle de temps représentant la durée de vie plausible du service).
Il serait difficile de résoudre un tel programme sous forme
analytique, même en utilisant comme nous l'avons fait des spécifications fonctionnelles
simples ; cependant il est aisé de le résoudre sous forme numérique en procédant par
simulation.
La stratégie d'offre répondant à une évolution donnée des
coûts de production comportera donc d'une part une chronique N(t) représentant la
qualité du service offert, d'autre part une chronique de prix p(t). L'offre d'un service
documentaire sur le Web sera donc évolutive, même si l’on ne tient pas compte des
conditions de concurrence propres à ce marché. Il est d'autant plus nécessaire
d'organiser cette évolution dès la conception même du service.
Différenciation du service
Nous avons jusqu'à présent supposé que le service était
offert sous une seule forme. Il est souvent intéressant, pour toucher divers segments de
clientèle, de différencier en " gamme " l'offre de services; la
différenciation peut porter soit sur le contenu de la base documentaire (plus ou moins
riche), soit sur le mode d'accès (plus ou moins confortable), soit sur les deux
caractéristiques. Le service de qualité moindre sera vendu à un prix plus bas.
Nous décrirons d'abord comment formaliser l'offre en gamme,
puis lui appliquerons le modèle précédent afin de représenter la réaction des clients
à une telle offre. Il en découle des indications relatives aux effets des stratégies
d'offre sur la diffusion d'un service.
Offre d’une gamme
Pour schématiser le cas où le service est offert en gamme,
nous supposerons que deux types d'accès et de stocks sont prévus :
- l'un concernant des documents stockés en mode caractère, et
offrant N1 documents à la consultation ;
- l'autre concernant des documents stockés en mode image (et
comprimés de façon que la durée de transmission soit analogue à celle des documents en
mode caractère), offrant N2 = 10 x N1 documents.
Deux services différents seront offerts :
- un service "bas de gamme" S1,
offrant le premier type d'accès seulement ;
- un service "haut de gamme" S2,
offrant les deux types d'accès.
Nous noterons N2 > N1 le nombre d'ouvrages
accessibles avec S2. U(N) étant fonction croissante
de N, U(N2) > U(N1).
Nous supposerons pour simplifier le raisonnement que ces deux
services sont vendus pour des prix forfaitaires p1 et
p2 avec p2 >
p1 (cette hypothèse sera enrichie par la suite pour
introduire des tarifications plus complexes).
Réaction des clients à une offre en gamme
Le client l
envisage de s'abonner si ul > 0, c'est-à-dire si pour l'un des deux services au moins p < U(N)/l. Il choisit ensuite celui des deux services qui
maximise ul.
Si pour des valeurs données de N1 et N2 l'on représente les valeurs de ul en fonction de l, on trouve le graphique suivant mettant en
évidence les seuils de décision :
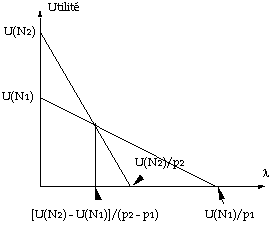
Graphique 14 : les seuils de décision
Supposons que U(N1)/p1 > U(N2)/p2 (sans cela, seul le service S2
pourrait avoir des clients).
Il résulte de la forme retenue pour la fonction d'utilité que
si, pour un client dont le paramètre est l :
(15)
(15) l <
[U(N2) - U(N1)]/(p2 - p1), client s'abonne à S2 ;
(16) [U(N2) - U(N1)]/(p2 - p1) <
2) - U(N1)]/(p2 - p1), client s'abonne à S2 ;
(16) [U(N2) - U(N1)]/(p2 - p1) < l <
U(N1)/p1, le
client s'abonne à S1 ;
(17) 1)/p1, le
client s'abonne à S1 ;
(17) l >
U(N1)/p1, le
client n'achète aucun des deux services.
En considérant la distribution des valeurs de
1)/p1, le
client n'achète aucun des deux services.
En considérant la distribution des valeurs de
l dans la population, on obtient la répartition
suivante :
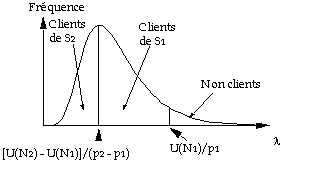
Graphique 15 : clientèles potentielles
Les surfaces contenues sous la courbe donnent les proportions
entre les effectifs des populations clientes de S1,
de S2 ou d'aucun des deux services. Ces surfaces
dépendent des valeurs N1 et N2,
ainsi que des prix p1 et p2.
Stratégie d'introduction d'une gamme
Les effectifs ainsi déterminés sont ceux des clientèles potentielles
des deux services : si l'on représente par une fonction de Gompertz la variation de la
clientèle d'un service dans le temps, l'effectif ci-dessus sera l'ordonnée de
l'asymptote.
Si l’on observe la façon dont se constituent les stocks
documentaires, on doit distinguer deux phases dans l’évolution de
l’offre : dans une première phase, les prix p1
et p2 seront stables et par contre N1 et N2 seront en croissance ;
dans une seconde phase, N1 et N2
seront stabilisés et les prix p1 et p2 décroîtront. La dynamique de pénétration des services sera
donc complexe : à l'effet pur de pénétration décrit par les logistiques s'ajouteront
les effets des variations de N1 , N2, p1 et p2 sur la position des asymptotes.
Dans la première phase, la croissance de U(N1) et de U(N2) provoquera un
déplacement vers le haut des deux droites du graphique 14 ; la pénétration de
l'ensemble des deux services augmentera, mais la pénétration de S2
dépendra du signe de la variation de U(N2) - U(N1). Si l'on suppose que U(N) = k. ln (N), U(N2)
- U(N1) reste constant si le rapport N2/N1 ne varie pas : dans ce
cas, la pénétration du service S2 ne varie pas non
plus dans la première phase ; par contre, celle du service S1
augmente.
Dans la deuxième phase, la diminution de p1 et p2 fait pivoter les
droites du graphique 14 autour de leur intersection avec l'axe des ordonnées. Si l'on
suppose que les baisses des deux prix se font dans les mêmes proportions, les effectifs
potentiels des deux services seront accrus.
Enrichissement de la tarification
Nous avons jusqu'ici supposé que la vente du service se
faisait, comme pour un magazine, à l'abonnement ou au numéro. La facture ne dépend donc
pas du volume de la consultation : le prix est une constante (F = p).
Il est généralement opportun de pratiquer un prix fondé pour
partie sur le volume V de la consommation. La formule de facturation contient alors un
degré de liberté supplémentaire (F = a + b.V), ce qui permet d'améliorer l'efficacité
(c'est-à-dire d'accroître l'utilité pour le client à profit égal ; cf ci-dessous).
L'accroissement de l'utilité favorise, pour une facture moyenne
égale, une meilleure pénétration du service. Elle permet donc une hausse du profit (ou
une baisse de prix permettant une pénétration encore accrue) en raison de l'importance
des coûts fixes dans ce type de service.
Tout se passe comme si, en remplaçant dans le raisonnement qui
précède le prix p par le montant F de la facture, on diminuait en même temps la valeur
de l (c'est-à-dire la sensibilité
au prix) pour chaque client. Ceci revient à tasser vers la gauche la distribution de la
population selon ce paramètre, et donc à augmenter la taille de la clientèle
potentielle pour un rapport U(N)/p donné.
Nous allons établir que la formule la plus efficace sera une
tarification dégressive (par exemple par paliers).
Démonstration
Supposons pour simplifier que les utilisateurs se classent en
deux catégories selon l'intensité de leurs besoins :
- A : besoins faibles ;
- B : besoins forts.
Nous supposerons que la fonction d'utilité est quasi-concave,
du type
(18) ui(V,F) = ui(V) - F, avec i = A ou i = B, F étant le
montant de la facture et V le volume de la consommation.
Supposons le coût de production du type K + c.V (K est le coût
fixe, c le coût marginal).
Notons D1 la droite F = c.V
et D2 la droite F = p.V (p = prix
"linéaire").
La condition d'équilibre budgétaire au prix p est, avec des
notations évidentes issues du graphique ci-dessous,
(19) MANA + MBNB
= K.
Soit D' la droite parallèle à D1
passant par MB.
Si on propose le tarif linéaire par morceaux (D2,D'), l'équilibre budgétaire est respecté et l'utilité est
accrue pour les consommateurs "forts".
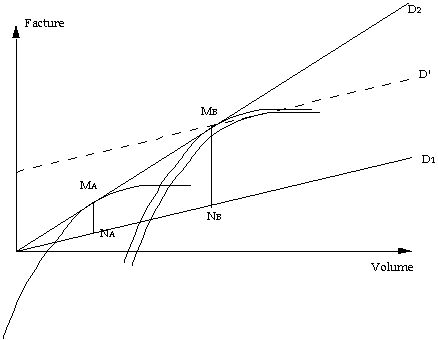
Graphique 16
L'augmentation de l'utilité est perçue par le client comme une
amélioration du rapport qualité/prix ; elle a pour conséquence, comme le montre le
graphique ci-dessus, une augmentation de la quantité consommée par l'utilisateur dont
les besoins sont forts. Elle entraîne aussi une hausse de la pénétration du service, la
hausse du rapport qualité/prix offert faisant franchir le seuil de décision à une
nouvelle fraction des utilisateurs potentiels.
Modèle économique
Les résultats ci-dessus permettent de construire un modèle
économique éclairant les politiques d'offre.
Supposons en effet que le comportement de la clientèle soit
conforme au modèle que nous venons de décrire, et que l'offreur ne puisse jouer que sur
le prix du service (la qualité est donc supposée constante). Baisser le prix lui permet
d'élargir la clientèle potentielle en fonction de la distribution du paramètre
l dans la population. La clientèle potentielle se
transformera ensuite en clientèle effective selon le rythme de pénétration permis par
la loi de Gompertz. L'évolution de la recette sera la résultante de deux effets de signe
contraire : baisse de la recette unitaire en raison de la baisse du prix, hausse du nombre
d'unités consommées. La connaissance des lois de comportement des clients (connaissance
que nous supposons ici acquise par l'offreur) lui permet de calculer cette résultante, et
donc de prévoir les chroniques de recettes correspondant à diverses politiques de prix.
L'offreur connaît par ailleurs les chroniques des coûts de
production (dépenses d'investissement et frais d'exploitation) correspondant à la
fourniture des volumes demandés pour le niveau de qualité retenu. Ces coûts de
production varient dans le temps, le coût unitaire étant fonction décroissante de la
quantité produite.
L'offreur est donc finalement en mesure de constituer la
chronique de la variation de trésorerie disponible (VTD) induite par une politique de
prix, en désignant par ce terme la fonction p(t) qui détermine l'évolution du prix du
service dans le temps.
Il peut ainsi associer à chaque politique de prix des
indicateurs comme la VAN (valeur actuelle nette), le TRI (taux de rentabilité interne) ou
tout autre indicateur synthétique, et faire son choix en connaissance de cause. Dans la
pratique, le choix effectif doit tenir compte du risque dû aux lacunes de l'information
et de contraintes dues au comportement des clients (il est ainsi en pratique difficile de
modifier un prix à la hausse, et p(t) sera donc une fonction décroissante au moins en
prix réel ; les changements tarifaires ne doivent pas intervenir trop souvent, et
p(t) sera donc une fonction évoluant par palier).
Le modèle informatique que nous venons de décrire, développé
sous Excel et exploitable sur un PC, permet de réaliser aisément les divers calculs que
nous venons de décrire. On doit entrer les paramètres de la loi Log-Normale et de la loi
de Gompertz, ainsi que la loi de U(N) permettant de déterminer le rapport qualité prix
U(N)/p. On entre ensuite la politique d'offre choisie (caractérisée par des chroniques
N(t) et p(t)), et le modèle établit la chronique de diffusion du service. C'est à
l'aide de ce modèle que nous avons établi par simulation les courbes de diffusion
présentées dans la note.
A partir de cette chronique, et en utilisant des hypothèses sur
les coûts de production du service, on peut effectuer les calculs permettant d'évaluer
la rentabilité dégagée par la politique d'offre considérée, et comparer des
politiques diverses.
Evaluation économétrique
Nous avons postulé ci-dessus que les comportements des clients
suivaient des lois de formes déterminées. Conformément à la méthode économétrique,
nous ne remettrons pas en question les formes de ces lois tant que nous n'aurons pas de
fortes raison de nous rallier à d'autres spécifications. Nous devons cependant nous
préoccuper de l'estimation des paramètres numériques qui permettent de définir ces
lois.
Le modèle ci-dessus ne peut être en effet utilisé de façon
réaliste qu'à la condition que l'on dispose d'estimations convenables des paramètres
des fonctions impliquées. Ces évaluations devront être faites de façon exploratoire au
moment de la préparation du service, puis mises à jour tout au long de son exploitation
en observant les comportements des clients. Il faudra déterminer dans l'ordre les
paramètres des lois suivantes :
- fonction d'utilité ;
- loi Log-Normale de distribution de
l ;
- loi de Gompertz.
Forme de la fonction d'utilité
On a supposé que U(N) = k.ln(N/N0).
Les paramètres k et N0
déterminent l'effet relatif des gains en qualité et des baisses de prix sur les
décisions des clients potentiels. Il est important de les connaître afin de déterminer
comment l'offreur devra doser ses efforts et pourra arbitrer entre la hausse du coût de
production nécessitée par une augmentation de la qualité et la baisse de recette
unitaire associée à une baisse de prix.
Par exemple pour évaluer k, il faudra s'efforcer de connaître
les équivalences que le client a en tête (considère-t-il qu'il est normal de payer deux
fois plus pour accéder à un stock de documents 3 fois plus grand, 10 fois plus grand, 20
fois plus grand etc ?).
Loi Log-Normale
Les paramètres de la loi Log-Normale de distribution des
valeurs de
- loi de Gompertz.
Forme de la fonction d'utilité
On a supposé que U(N) = k.ln(N/N0).
Les paramètres k et N0
déterminent l'effet relatif des gains en qualité et des baisses de prix sur les
décisions des clients potentiels. Il est important de les connaître afin de déterminer
comment l'offreur devra doser ses efforts et pourra arbitrer entre la hausse du coût de
production nécessitée par une augmentation de la qualité et la baisse de recette
unitaire associée à une baisse de prix.
Par exemple pour évaluer k, il faudra s'efforcer de connaître
les équivalences que le client a en tête (considère-t-il qu'il est normal de payer deux
fois plus pour accéder à un stock de documents 3 fois plus grand, 10 fois plus grand, 20
fois plus grand etc ?).
Loi Log-Normale
Les paramètres de la loi Log-Normale de distribution des
valeurs de l pourront être évalués
lors d'une enquête auprès des utilisateurs potentiels, qui permettra de situer pour
chacun d'entre eux le seuil critique et de déterminer ensuite la distribution de ce seuil
dans la population.
Loi de Gompertz
Les paramètres de la loi de Gompertz devront être choisis au
départ de façon raisonnable, compte tenu de l'expérience acquise sur des services
analogues ; il sera possible par la suite de préciser ces évaluations à partir de
données d'observation.
Conclusion
La démarche décrite dans cette note permet de rendre compte de
divers aspects de la diffusion d'un nouveau service. Le modèle économique facilite la
réalisation des calculs. Il s'agit donc d'un outil complet dans son domaine.
Pour autant, des limites subsistent. Les spécifications
retenues pour les diverses lois (fonction d'utilité, distribution de la sensibilité au
prix, loi de pénétration) sont plausibles, mais pourraient être affinées pour tenir
compte de situations concrètes. Le modèle a été simplifié pour ne retenir que les
phénomènes essentiels : les applications doivent tenir compte des complications que
peuvent présenter les cas particuliers.
Le point le plus faible est la partie économétrique. Nous
n'avons pas procédé aux recherches statistiques et aux estimations qui permettraient de
compléter le raisonnement qualitatif par des mesures. Il est par ailleurs évident que
les études de marché ne donneront que des indications imprécises sur les préférences
des clients et sur la fonction d'utilité.
Enfin les aspects tarifaires, ainsi que les problèmes liés à
la différenciation en gamme, ont été abordés mais non traités à fond.
Au total cette note donne un cadre de raisonnement, et de ce
point de vue elle est complète puisqu'elle aborde les aspects essentiels du problème
posé. Cependant il faudra pour les applications l’enrichir en prenant en compte les
caractéristiques propres au service considéré. Il faudra aussi faire un effort pour
quantifier les évaluations de la manière la plus plausible, et rectifier ces
évaluations en fonction des données apportées par l'expérience après lancement du
service.
|