(Cf. Jean-Marc Jancovici, " Le réchauffement climatique, réponse à quelques questions élémentaires ", La Jaune et la Rouge, mai 2000.)

On entend souvent mettre en doute la réalité de l’effet de serre, à partir de l’argument suivant : " personne n’a pu démontrer que la hausse actuellement constatée de la température moyenne de la planète était due à l’effet de serre, car on ne peut pas, statistiquement, la distinguer de celles qui ont eu lieu historiquement soit par variation aléatoire, soit par variation cyclique ".

Le fait évoqué par cette argumentation est exact, et pourtant il porte à faux : il ne démontre nullement que l’effet de serre n’existe pas.

L’examen des " carottes " extraites des glaces polaires permet de connaître avec exactitude l’évolution historique de la proportion des gaz à effet de serre dans l’atmosphère :

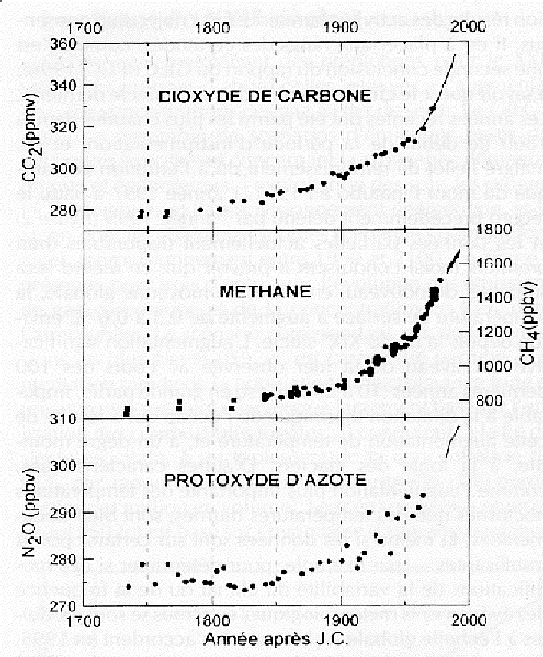
Il apparaît clairement que la proportion de dioxyde de carbone (CO₂, le principal gaz à effet de serre) croît exponentiellement depuis le milieu du XVIIIème siècle, c’est-à-dire depuis le début de la révolution industrielle et de la consommation intensive de combustibles fossiles qui l’a caractérisée.

La durée de vie du CO₂ dans l’atmosphère est de 100 ans ; pour pouvoir faire diminuer sa proportion, il ne suffirait pas de faire cesser la croissance des émissions, car la proportion va croître si l’on émet plus de CO₂ que les océans ne peuvent en absorber (D'après le GIEC, la biosphère sait absorber une émission de 3 Gt/an d’équivalent carbone. La quantité actuellement émise est de 6 Gt/an). Les programmes politiques actuellement en discussion sont donc très timides en regard des exigences de la situation : il est vrai qu’il est très difficile d’infléchir une exponentielle.

La croissance industrielle des pays pauvres, notamment de la Chine, souhaitable à tous les autres égards, va avoir pour effet au contraire d’accélérer la diffusion de CO₂ dans l’atmosphère, et donc de continuer la croissance exponentielle de sa proportion.

Les spécialistes ont construit plusieurs modèles permettant de simuler l’évolution de la température moyenne de la planète ; ces modèles donnent des résultats divers, mais tous indiquent une hausse significative, comme le montre le graphique ci-dessous où l’on a représenté tous les résultats des simulations :

L’augmentation future de la température est donc certaine, contrairement au raisonnement indiqué au début de cette annexe. Elle aura d’importantes conséquences géopolitiques, à côté desquelles les tensions que connaît actuellement la planète (Yougoslavie, Moyen Orient, Rwanda et Burundi) apparaîtront bien peu de choses.

Nous allons pour notre part simuler le réchauffement de la planète en utilisant le petit modèle suivant :

Notons R le rayonnement reçu par la terre (342 W/m²), R’ le rayonnement qu’elle réémet.

Supposons que R’ soit fonction de la température moyenne t de la terre et de la concentration c du CO₂ dans l’atmosphère, de la forme :

R’ = at - bc + e, avec a et b positifs. 

Pour ce modèle, nous supposons que toutes les fonctions sont affines : cela revient à supposer que l’on est dans le domaine des petites variations, et que l’approximation d’une fonction par son développement d’ordre un est valable. Cette approximation n’est pas acceptable si (a) les variations considérées des variables exogènes sortent de la zone où le développement d’ordre un est acceptable ; (b) il existe des effets de seuil rompant la continuité de la fonction. Le modèle représente donc une première exploration qui serait à compléter pour tenir compte de ces deux limitations.

La valeur observée de c était de 280 ppmv (parties par million en volume) jusqu’en 1800, de 300 ppmv en 1900 et de 380 ppmv en 2000, soit une croissance moyenne de 0,24 % par an pendant le XXème siècle.

Si R’ = R, la température reste au même niveau t. La température d’équilibre est donc t telle que :

R = at - bc - e, soit :

t = (R + bc - e)/a

Il en résulte la conséquence attendue : la température d’équilibre est d’autant plus élevée que la concentration c en CO₂ est plus forte.

Supposons que l’accroissement annuel de la température est fonction linéaire du rayonnement " piégé " R - R’ :

Dt = f(R - R’) = af(t - t).

Nous voulons, pour rendre le modèle réaliste, respecter deux contraintes censées résumer l’expérience :

• les modèles montrent que si la concentration de C0₂ montait de 1 % par an, cela entraînerait un réchauffement de 1°C.

• nous supposerons que la température moyenne avec une concentration de CO₂ de 280 ppmv est de 10°C.

Nous prendrons les paramètres suivants, ajustés de façon à respecter les deux contraintes précédentes :

Il en résulte les évolutions suivantes : si l’on suppose que la concentration en CO₂ passe brusquement de 280 à 290 ppmv (hypothèse irréaliste, mais que nous essayons " pour voir "), l’évolution de la température moyenne de la terre a l’allure suivante :

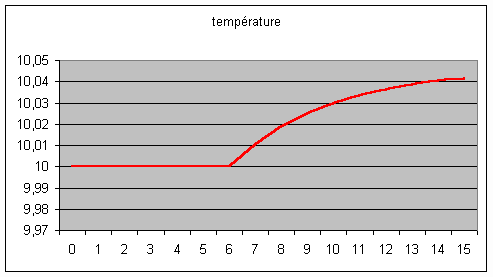
La moitié de la hausse de la température se produit en trois ans (la vitesse de cette convergence dépend de façon cruciale du coefficient f, ici égal à 0,005).

Supposons que dès l’année 1 la concentration de CO₂ se mette à croître de 0,24 % par an. Il en résulte une augmentation régulière de la température moyenne :

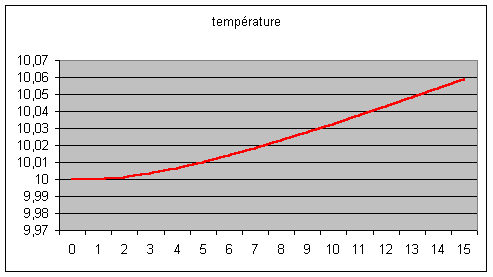
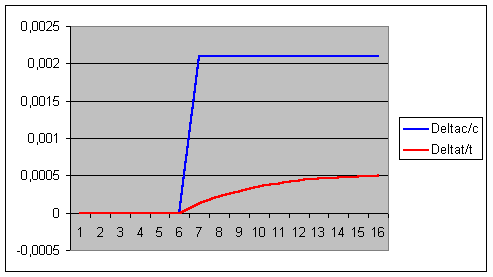
La hausse de la température a un léger retard par rapport à celle de la concentration en CO₂, puis les deux rythmes se stabilisent. L’augmentation de la température limite se fait à un rythme qui est, au décalage près entre la température constatée et la température limite, fonction croissante de la concentration du CO₂ car :

Dt/t = [bc/(R + bc)] Dc/c