Erreurs dans les présentations des données statistiques

Voici plusieurs erreurs classiques. Certaines ont pour but de distordre l’information à des fins intéressées ou partisanes ; d’autres sont dues à l’ignorance.

Erreur sur les tendances

Lorsqu’une série est fortement fluctuante, prendre pour estimer la tendance un point bas du passé lointain, comparé à un point haut du passé récent, peut faire apparaître une croissance alors que la tendance est à la baisse.

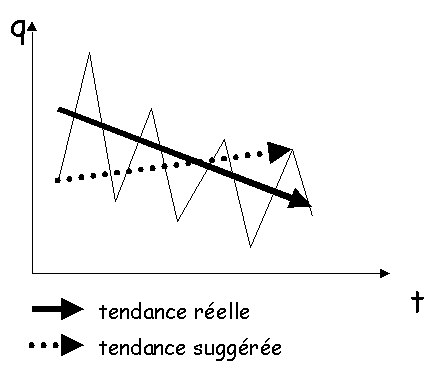
Remède : supprimer les fluctuations par un lissage ou par une correction des variations saisonnières.

Estimation de la tendance par comparaison à l’année passée

Certains aiment bien, pour évaluer la tendance, comparer le nombre du dernier mois connu avec celui du mois correspondant de l’année précédente. C’est ce que l’on appelle le " R/R " (pour " réalisé sur réalisé ", par différence avec " R/P " qui veut dire " réalisé sur prévu ").

Variantes de cette méthode : considérer non la valeur du mois, mais

• la valeur cumulée depuis le début de l’année,
• la somme des valeurs sur les douze derniers mois,
• etc.

Certains croient que cette méthode convient bien pour corriger les effets saisonniers. Mais même si elle fournit une courbe qui semble facile à lire, elle est fallacieuse. Obtenue en divisant les valeurs récentes par celles de l’année d’avant, elle recouvre deux conjonctures au lieu d’une seule, et les superpose de telle sorte que l’on ne peut plus les séparer. Il est facile de montrer qu’une même courbe R/R recouvre des évolutions très différentes en modifiant les mois de la première année :

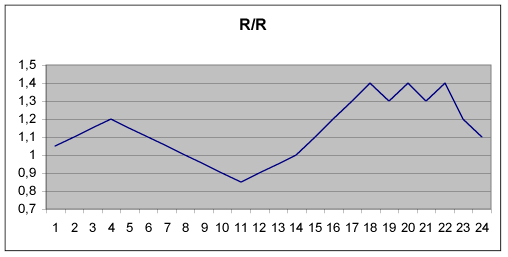
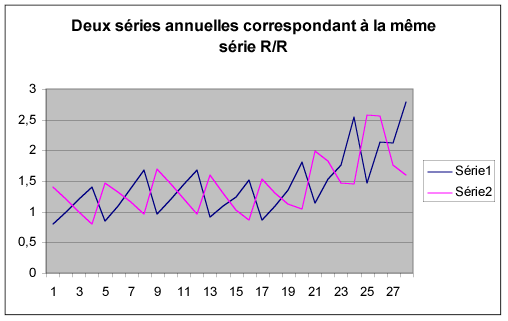
Le caractère trompeur de cette méthode, l’incertitude qu’elle introduit dans l’interprétation, ne l’empêchent pas de plaire à ceux qui la trouvent " plus simple " et " plus facile à interpréter " que les séries corrigées des variations saisonnières. Pourtant, même si la CVS est conventionnelle et comporte une part d’incertitude, au moins elle ne ment pas. Il ne faut pas hésiter à dire à ces personnes : " Une voyante donne des indications claires, mais sont-elles exactes ? ".

Utiliser une courbe au lieu d’un histogramme

Quand on veut comparer des données relatives à des régions, ou à des produits etc. il vaut mieux utiliser un histogramme qu’une courbe : en effet, comme la position des points représentants les diverses régions, produits etc. sur l’axe des x est arbitraire, la pente que ferait apparaître une courbe n’a pas de sens.

J’ai pourtant vu commenter la pente d’une courbe sur un graphique représentant des chiffres d’affaires par région.

Se tromper d’échelle

Si vous superposez sur un même graphique deux courbes obéissant à des échelles différentes, attention ! il se peut que la série qui croît le plus vite apparaisse moins pentue que l’autre. Sur le graphique ci-dessous, l’échelle de gauche est relative à la série rouge, l’échelle de droite à la série bleue ; et en réalité, la série rouge croît plus vite que la série bleue.

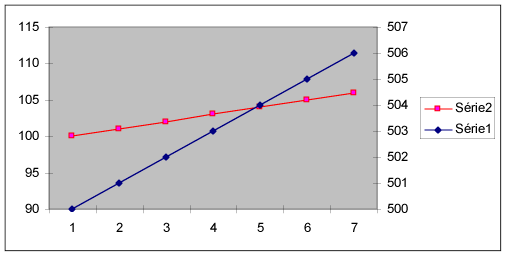
Remède : caler la valeur zéro de chaque variable sur une ligne identique située en dessous du graphique.

Un " fromage " hors de saison

Les " fromages " sont faits pour visualiser des répartitions en pourcentage à l’intérieur d’une quantité (par exemple, le chiffres d’affaire par produit, la population par région, etc.). Il ne faut pas les utiliser pour visualiser des ratios (consommation par tête dans diverses régions, prix unitaire par produit), qui seront mieux visualisés par un histogramme.

Un rythme de croissance non lisible

Si on représente graphiquement une série qui croît rapidement, on ne voit sur le graphique qu’une exponentielle peu lisible. Pour faire apparaître les changements de tendances, il faut soit la représenter sur papier semi-logarithmique (une croissance à taux constant est alors représentée par un segment de droite) ou par un graphique en taux de croissance, qui sera parfois le plus lisible.

C’est ainsi que l’indice du prix des micro-ordinateurs, dont la diminution est très rapide, est peu lisible sous sa reproduction graphique simple, qui ne montre qu’une exponentielle décroissante.

Autres erreurs

Appliquer l’analyse des correspondances à un tableau qui n’est pas, de près ni de loin, " de contingence " ; c’est la même erreur que pour le " fromage " évoqué ci-dessus. Cependant certains tableaux, comme ceux fournis par un codage disjonctif complet, sont " de contingence " au sens large.

Appliquer une régression à deux séries chronologiques, et croire qu’elles sont corrélées, alors qu’elles sont toutes deux corrélées avec le temps.