|
Économie du dimensionnement
11 juin 1999
Cette fiche a pour origine une remarque de Michel Matheu, du
Commissairiat général du Plan, qui s’interrogeait sur la pertinence d'une fonction
de production à coût fixe pour rendre compte de l’économie du transport aérien
(et, plus généralement, de l'économie d'un réseau).
Cette remarque m’a conduit à traiter de façon plus
précise certaines propriétés de l’économie des réseaux ; la présente fiche
a vocation à compléter le chapitre consacré à ce sujet dans " Economie des nouvelles technologies ".
L’économie d’un réseau n’est en effet
qu’à demi " à coût fixe ". Pour la représenter de façon
simple, nous supposerons, en illustrant la théorie par l'exemple du transport
aérien :
- Que le coût de dimensionnement est fonction linéaire de la dimension D du
réseau, D étant mesurée par le nombre de sièges*kilomètres offerts (SKO), ou encore
en pondérant les SKO selon le type de l’avion et la longueur des escales, mais peu
importe ici.
- Que le coût d’exploitation est un coût fixe, indépendant jusqu’au
seuil D du nombre de passagers*kilomètres transportés (PKT), et infini si le nombre de
PKT dépasse D (cela revient à supposer qu'il est impossible d'affréter des avions
supplémentaires en cas de besoin, hypothèse que l'on peut juger trop forte ; on pourrait
l'éviter en supposant que le coût d'une offre supplémentaire de dimensionnement est
élevé, ce qui est vrai ; dans ce cas, l'on aurait au delà du seuil D un coût
d'exploitation représenté par une demie droite de pente non infinie, mais élevée).
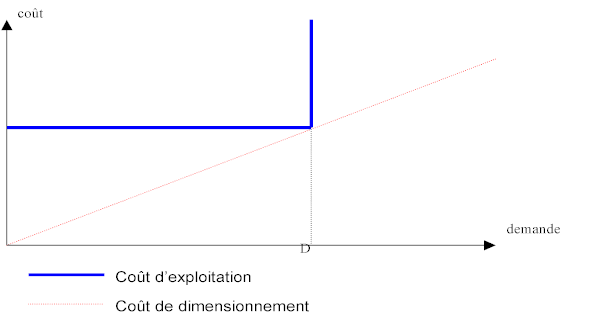
Dès lors on peut représenter la fonction de coût par deux
fonctions :
- coût de dimensionnement
, mesuré par l’équivalent quotidien ( en
valeur actualisée) du coût des investissements et des frais de personnel nécessaires au
dimensionnement : C = aD
- coût d’exploitation (quotidien)
: c est égal à C si la demande
est inférieure à D, c est infini si la demande est supérieure à D.
Dans le coût de dimensionnement on compte le salaire des personnels qui sont
nécessaires pour faire fonctionner les installations, et donc pas seulement le coût
d'investissement en capital fixe.
NB : On peut utiliser le même schématisme pour représenter le
coût d'un réseau de télécommunications : ce coût dépend de la capacité du réseau
à acheminer un nombre D de communications. Une fois le réseau dimensionné, son coût a
été payé, et il sera le même quel que soit le nombre de communcations pourvu qu'il
soit inférieur ou égal à D. Le réseau est incapable d'acheminer davantage de
communications (les appels supplémentaires sont refoulés), et donc le coût
d'exploitation de court terme est infini au delà de D. Un raisonnement analogue peut
être fait sur le dimensionnement d'un réseau routier, d'un réseau de transport
maritime, d'un réseau d'adduction d'eau etc.
Nous supposerons que le transporteur exploite une ligne à
fréquence quotidienne : prendre en compte la multiplicité des lignes, la structure
en " hub and spokes ", les fréquences etc. n’apporterait rien au
raisonnement que nous voulons construire ici (même si ces aspects ont par ailleurs une
incidence notable sur les coûts).
La demande de transport aérien est ici représentée par une
série chronologique quotidienne ; la demande xt du jour t peut être
simulée par un tirage aléatoire dans une loi de Laplace-Gauss N(m, s), dite "loi Normale", de
fréquence :
(1) f(x) = s -1 (2p)-
1/2 e - (1/2)[(x – m)/s]2 - (1/2)[(x – m)/s]2
(En toute rigueur, il faudrait prendre une loi Log-Normale,
puisque le nombre de passagers ne peut pas être négatif ; cependant la loi Log-Normale
peut être correctment approchée par une loi Normale lorsque m est très supérieur à
s, ce que nous supposons ici).
Si xt < D, tous les passagers peuvent être
transportés.
Si xt > D, il faut renoncer à transporter une
partie des passagers.
Calcul du nombre moyen de passagers
Le nombre moyen M de passagers transportés est non pas m,
puisque la moyenne m recouvre aussi les jours où xt > D, mais, en notant
F(x) la fonction cumulative de f(x) :
(2) M = ò 0<Dxf(x)dx
+D[1 – F(D)] < m
le calcul fournit le résultat
suivant :
(5) M = D[1 – F(D)] + mF(D) –
s2 f(D)
(NB : Il est facile de vérifier que si s -> 0, M -> m : en effet alors D ->
¥ , f(D) -> 0 et F(D) -> 1).
Dimensionnement optimal
Cherchons le dimensionnement D* qui maximise le profit lorsque m
et s sont donnés. La recette est
proportionnelle au nombre de passagers transportés ; le profit est donc, en notant p
le prix du billet :
(6) P = pM
– aD
Si a, p, m et
Si a, p, m et s sont donnés, le calcul montre que D* est tel que :
(7) 1 – F(D*) = a / p
Le terme de gauche de cette équation est égal à 1 lorsque D*
= 0 (parce que s est supposé petit
par rapport à m). Il est décroissant lorsque D* croît, égal à 0,5 lorsque D* = m,
puis il tend vers zéro lorsque D* -> ¥ .
La position de D* par rapport à m dépend donc du rapport a /
p, rapport entre le coût unitaire du dimensionnement et le prix unitaire du billet :
- si a / p > 0,5, D* < m ;
- si a / p = 0.5, D* = m ;
- si a / p < 0,5, D* > m.
Ce résultat peut surprendre : on s’attendait en effet
a priori à ce que D soit systématiquement supérieur à m.
L’équation (7) a une et une seule racine si a / p < 1.
Comme f(D*) > 0, la dérivée seconde du profit est négative : il s’agit donc
bien d’un maximum.
Il n’est pas possible de résoudre analytiquement
l’équation (7) ; les abaques ci-dessous permettent de visualiser la solution.
Supposons par exemple que a = 5, p = 10, m = 10 et s = 2. L’évolution du profit en fonction de
D est la suivante (NB : cette courbe dépend de a, p, m et s) :
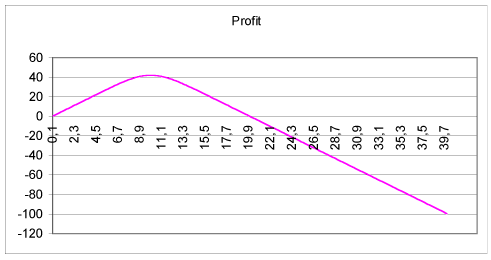
Le profit maximal est atteint pour D* = 10 (c'est normal puisque
avec les hypothèses retenues a / p = 0,5).
Le taux de remplissage moyen en fonction de D (rapport M/D) est
le suivant (NB : cette courbe dépend de m et de s):
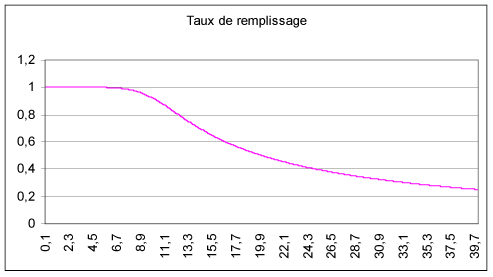
Le taux de remplissage moyen est de 92 % si D = D*=10.
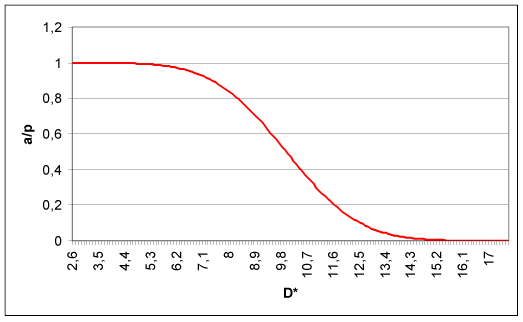
Les valeurs de D* en fonction du rapport a/p sont indiquées par
le graphique suivant (NB : cette courbe dépend de m et de
s) :
|