Cette fiche décrit l'équilibre de
concurrence monopoliste d'un
produit dont les consommateurs demandent diverses variétés, en distinguant deux
cas :
1) les variétés ont toutes le même coût de production (qualité "horizontale") ;
2) le coût de production est fonction croissante de la qualité du produit
(qualité "verticale").
1 - Qualité « horizontale »
Considérons un produit susceptible de
diversification, c’est-à-dire tel que les besoins des consommateurs soient
divers : ils ont des goûts différents.
Posons les hypothèses suivantes :
1) Il existe
N consommateurs.
2) Les
besoins des consommateurs se différencient selon un paramètre x réparti
uniformément sur l’intervalle (0,1).
3) Le coût
fixe à dépenser pour offrir une variété du produit est C ; ce coût fixe recouvre
les dépenses de conception, mise en fabrication, ainsi que le service associé à
la commercialisation du produit. L’expression « coût fixe » signifie que C est
indépendant de la quantité produite comme de la quantité vendue.
4) Le produit
est tel que chaque consommateur en achète un exemplaire ou aucun.
5) La
fonction de demande se résume à l'existence d'un prix de réservation P.
6) Le
consommateur dont la variété préférée est x' achètera le produit s'il existe une
variété x offerte au prix p et telle que p + |x – x’| < P.
On peut, dans l'espace des besoins, représenter
la zone de chalandise de la variété x par le graphique suivant :
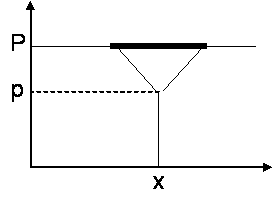
Le nombre d’unités vendues de cette variété est y
= 2N (P – p), où N est le nombre de consommateurs. Le chiffre d’affaires du
producteur est yp.
Si yp > C, l’offre de la variété x dégage du
profit. La libre entrée suscitera alors l’offre d’autres variétés dont les zones
de chalandise vont paver l’intervalle (0,1) jusqu’à ce que le profit soit nul.
Il en résulte qu'à l'équilibre le prix est p* tel que
yp* = 2Np*(P – p*) = C
d’où l'équation en p*
p*2 - Pp* + C/2N = 0
Seule une des deux solutions de cette équation
correspond à un équilibre stable, et elle n’existe que si C < NP2/2.
Posons A = (P2 – 2C/N)½ ;
alors
p* = (P + A)/2
Lorsque la libre entrée est parvenue à son terme,
l'intervalle (0,1) est entièrement pavé par l'offre. Le nombre n* de variétés à
l’équilibre est tel que chaque consommateur achète une unité du produit
n*y = N, d'où
n* = 1/2(P – p*) = 1/(P - A)
(NB : plus exactement, n* est la partie entière
de cette quantité)
n* est fonction croissante de P et fonction
décroissante de C. Comme le coût fixe C recouvre essentiellement des salaires,
l’emploi à l’équilibre est
E* = n*C, d'où
E* = C/(P - A)
2 - Qualité « verticale »
Considérons maintenant la qualité « verticale »,
qui distingue les produits selon leur degré de finition. Pour aborder cette
qualité du point de vue macro-économique, imaginons une robinsonnade. Robinson,
seul sur son île, dispose d’une ressource, son temps de travail. Il peut
l’utiliser pour produire un bien unitaire Y. Plus il travaille, plus la qualité
de Y est élevée ; plus cette qualité est élevée, plus il est satisfait mais le
travail comporte une désutilité. La fonction d’utilité de Robinson est U(W, Q),
croissante en fonction de Q et décroissante en fonction de W. La fonction de
production de la qualité est Q = Q(W).
On peut supposer de façon « réaliste » que Q(W)
est à rendement décroissant. L’équilibre s’établit au point (W*, Q*) qui
maximise U(W, L) sous la contrainte Q = Q(W) :
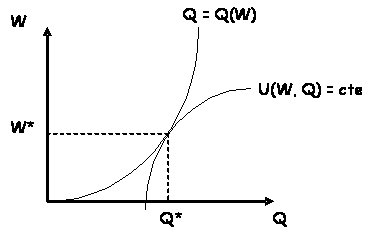
Ce raisonnement sommaire indique comment
endogénéiser la qualité verticale : il faut définir une fonction de production
qui associe un coût à la qualité, et une fonction d’utilité qui comporte la
qualité comme argument.
Reprenons le modèle ci-dessus et ajoutons lui les
hypothèses suivantes :
1) la qualité
est mesurée par un indice Q ∈ [0, 1] et la
population des N clients, repérés chacun par la qualité qu’il préfère, est
uniformément répartie sur cet intervalle.
2) à chaque
client est associé un prix de réservation P, fonction croissante de la qualité
qu’il préfère : P = P(Q), P’(Q) > 0, P’’(Q) ≤ 0. On peut expliquer cette
situation soit par la diversité des goûts, certaines personnes étant moins
sensibles que d’autres à la qualité (donc moins disposées à payer cher un
produit de haute qualité), soit par l’écart des revenus, les personnes ayant
toutes les mêmes goûts mais n’ayant pas toutes les moyens de s’offrir un produit
de haute qualité.
3) le coût de
production C est lui aussi fonction croissante de la qualité et le rendement de
la fonction de production de la qualité est décroissant : C = C(Q), C’(Q) > 0,
C’’(Q) > 0.
(NB : dans les calculs numériques, nous
retiendrons des fonctions de la forme C(Q) = kemQ et P(Q) = aQ + b)
Supposons qu’une variété de qualité q soit
offerte au prix p. Elle est susceptible de satisfaire les personnes pour
lesquelles la qualité préférée est Q telle que :
|Q – q| + p < P(Q).
Cela revient à supposer, comme me l'a fait
remarquer Nicolas Curien, qu'à chaque niveau de
qualité est symboliquement associée une catégorie de la segmentation sociale :
la personne qui pourrait acheter un produit de haute qualité à un prix
correspondant à ses moyens hésitera à le faire, par crainte de se faire mal voir
par les autres personnes de son segment. Nous explorerons ci-dessous une autre
hypothèse.
Notons e(q) la largeur de l’intervalle dans
lequel cette condition est remplie ; si l’on suppose que P’(Q) < 1 et que P’(Q)
varie peu dans cet intervalle, on trouve :
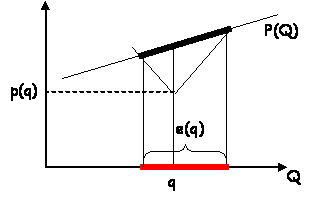
e(q) = 2 [P(q) – p] / [1 – P’(q)]
à l’équilibre le profit est nul, c'est-à-dire que
p est égal à p* tel que :
p* N e(q) = 2 N p* (P – p*) / (1 –
P’) = C(q)
ce qui donne, en posant A(q) = [P2(q)
– 2[1 – P’(q)]C(q)/N]½
p*(q) = [P(q) + A(q)]/2
On trouve, en reportant cette valeur dans
l’équation qui détermine e(q),
e*(q) = [P(q) – A(q)] / [1 – P’(q)]
La densité du nombre de variétés au point q étant
1 / e*(q), le nombre de variétés à l’équilibre est :
n* = ∫(0,
1)dq / e*(q)
Les trois relations ci-dessus donnent le prix
auquel est offert une variété, la largeur de son marché et le nombre total de
variétés. L’équilibre de concurrence monopoliste est ainsi entièrement défini.
Contrairement au modèle de la qualité
horizontale, il n’est pas possible ici d'effectuer l'ensemble du calcul de façon
analytique. Par contre on peut faire une simulation numérique : nous en donnons
ci-dessous un exemple.
Non
segmentation sociale
Supposons maintenant que les divers niveaux de
qualité du bien ne soient pas symboliquement attachés à un segment de la
société. Dans ce cas, une variété q offerte au prix p est susceptible de
satisfaire les personnes dont la variété préférée est Q telle que :
max {(Q - q), 0} + p < P
Cette expression se justifie ainsi :
- si le client est tel que pour lui Q > q, il achètera la variété q si Q – q +
p(q) < P(Q) ;
- si Q < q, le client achètera q si p(q) < P(Q).
L'intervalle e(q) a la forme suivante :
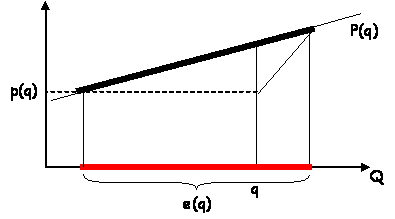
on trouve alors
e(q) = [P(q) – p] / P’(q) [1 –
P’(q)]
et si l'on pose
B(q) = [P2(q) – 4P’(q)[1
– P’(q)]C(q)/N]½
il vient
p*(q) = [P(q) +
B(q)]/2
e*(q) = [P(q) –
B(q)] / 2P’(q)[1 – P’(q)]
Simulation numérique
La simulation ci-dessous porte sur le cas où il
existe une segmentation sociale. Supposons que :
C(q) = 500*e0,7*q
P(q) = 0,1*q + 0,1
N = 400 000
On trouve les résultats suivants :
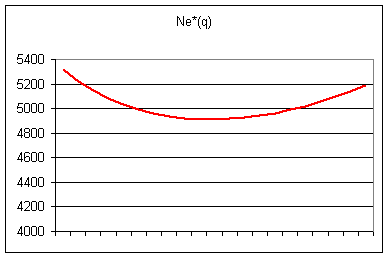
Largeur des parts de marché
Les segments de marché sont larges pour les
qualités faibles et fortes ; ils sont moins larges pour les qualités moyennes
(ce résultat dépend des valeurs retenues pour les paramètres et il n’a pas de
portée générale).
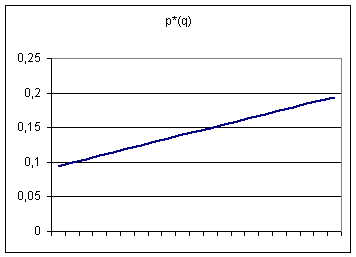
Prix en fonction de la qualité
Le prix d'équilibre est un peu plus bas que le
prix de réservation pour chacune des valeurs de q.
Enfin, le nombre de variétés est n* = 83.
3 - Conséquences d’un gain de productivité
Dans une économie où l'on ne considère que la
quantité et où, par hypothèse, les produits ne sont pas diversifiés en variétés,
la hausse de la productivité entraîne à l'équilibre concurrentiel une baisse du
prix. L'effet final sur l'emploi dépend de l'élasticité de la demande au prix,
et il peut donc être négatif.
Nous allons montrer que dans l'économie de la
qualité un gain de productivité se traduit par davantage d'emplois, résultat
qui la distingue nettement de l'économie de la quantité à laquelle nous sommes
habitués. Pour illustrer ce résultat nous nous limiterons à la diversification
horizontale.
NB : Je n'ai pas encore vérifié si ce résultat
avait ou non une portée générale (que devient-il si, par exemple, on remplace la
fonction linéaire |Q - q| par une fonction quadratique ?) Le résultat obtenu
avec notre spécification, qui est l'une des plus simples que l'on puisse
retenir, me semble toutefois devoir retenir l'attention.
* *
Quel est l'effet d'un gain de productivité dans
une économie où les produits sont diversifiés en variétés ? Le gain de
productivité permet soit (1) de diminuer le coût fixe C d’une variété, soit (2)
d’augmenter la qualité d’une variété. Il revient aux entreprises de doser ces
deux effets.
1) Supposons que leur politique soit de diminuer
C. Il en résulte une baisse de l’emploi nécessaire pour produire une variété,
mais aussi une hausse du nombre de variétés : l’effet sur l’emploi E* = n*C est
donc qualitativement ambigu.
L’effet quantitatif est éclairé par l’équation E*
= C/(P - (P2 – 2C/N)½). Si l’on suppose C/N petit par
rapport à P (ce sera le cas si le nombre de variétés est grand), un
développement limité de cette expression donne :
E* ~ NP – C/2P
: l'emploi total croît donc si C diminue.
Donc un gain de productivité sur un produit
fortement diversifié aura, même s’il est entièrement consacré à la baisse de C,
un effet positif sur l’emploi car l'accroissement du nombre des variétés fait
plus que compenser la baisse de l'emploi nécessaire pour produire une variété.
2) Supposons que C reste constant et que la
totalité du gain de productivité soit consacrée à une hausse de la qualité du
produit. Il en résulte une hausse du prix de réservation P. Elle entraîne une
hausse du nombre de variétés n* et une hausse de l’emploi total n*C.
Donc si le nombre des variétés est élevé, un
gain de productivité aura dans tous les cas un effet positif sur l’emploi.
|