Modélisation économique du système d'information

2 février 2002

Introduction

Le but de cette fiche est de fournir des simulations de la dynamique d’un système d’information (SI) lorsque l’entreprise détermine l’effort qu’elle consacre à celui-ci en suivant une des règles simples que l'on rencontre parfois dans la pratique des entreprises. 

Les directions générales perçoivent en effet souvent leur « informatique » comme un poste de coût qu’il faut comprimer, sans s’interroger plus avant sur la rentabilité du SI qu’elles croient d'ailleurs impossible à évaluer. Elles choisissent alors de suivre l’une ou l’autre de quelques règles simples : fixer le budget de l’informatique à un montant jugé raisonnable, qu'elles appellent "enveloppe", fixer la part des études dans le budget informatique etc. 

Toutefois certaines de ces règles sont susceptibles d’avoir des effets pervers que nous allons décrire.

Modèle

On pose les hypothèses suivantes :

-          le SI comporte à la date t un stock d’applications dont le volume [1] est mesuré par S_t, le coût de maintenance et d’exploitation par a_tS_t [2],

-          durant l’année t sont réalisées de nouvelles applications qui viendront s’ajouter aux anciennes et dont le coût de production est b_tN_t. (NB : Nous comptons parmi les nouvelles applications les évolutions des applications anciennes).

-          le taux d’obsolescence du stock d’applications anciennes est δ (0 < δ < 1) [3].

-          les coûts unitaires décroissent au taux annuel constant [4] k : a_t = ae^-kt, b_t = be^-kt

Le coût du SI à l’année t  est alors :

C_t  = a_tS_t + b_tN_t = (aS_t  + bN_t)e^-kt

Le stock d’applications en exploitation durant l’année t + 1 est :

S_{t + 1} = S_t + ΔS_t = S_t(1 - δ) + N_t

Si l’on connaît le niveau initial S₀ et la série N_t, on peut à partir des relations précédentes calculer les séries S_t et C_t. Les deux équations ci-dessus permettent donc, une fois posés le niveau S₀ et l’hypothèse concernant la série N_t, de décrire entièrement la dynamique du coût du SI.

D’après Peter Keen (1993), pour une dépense de 1 $ en développement, on dépense pendant chaque année ultérieure 20 cents d’exploitation et 40 cents de maintenance. Nous retiendrons ici les hypothèses suivantes :

-          le coût annuel de la maintenance est de 20 % du coût de réalisation (moyenne entre le taux initial de 15 % et le taux de 30 % au delà duquel l’application serait jugée obsolète),

-          le coût annuel d’exploitation est de 30 % du coût de réalisation.

Si l’on normalise le coefficient b (coût unitaire de la réalisation) en lui donnant la valeur 1, le coefficient a (coût unitaire de l’exploitation et de la maintenance) est donc égal à 0,5 ; le coût d’exploitation est alors 0,3*S_te^-kt et le coût des études (N_t + 0,2*S_t)e^-kt.

Les simulations seront réalisées à partir des hypothèses suivantes :

a = 0,5 ; b = 1 ; δ = 20 % (durée de vie = cinq ans) ; k = 20 %

Dynamique induite par des règles simples

Nous allons examiner l’évolution du budget informatique sous diverses hypothèses déterminant chacune la série N_t :

-          volumes constants :

-          constance du volume du stock S_t des applications ;

-          constance  du volume du flux N_t des nouveaux développements.

-          valeurs constantes :

-          constance  de la valeur du flux b_tN_t des nouveaux développements ;

-          part constante des nouveaux développements dans le budget ;

-          budget total constant.

Chacune de ces « règles simples » est en effet retenue par des entreprises. Certaines d’entre elles induisent des évolutions exponentielles (croissantes ou décroissantes). Les entreprises qui les appliquent peuvent certes, en pratiquant une régulation, changer la règle lorsque ses conséquences deviennent déraisonnables. Mais il faut pour cela qu’elles soient vigilantes : si une règle est appliquée quelques années de trop avant que l’entreprise ne réagisse, les dégâts peuvent être considérables. Réguler en appliquant une succession de règles explosives comporte des risques.

Volumes constants

Nous supposerons d’abord constant  le stock des applications en exploitation: les nouveaux développements compensent alors exactement la perte due à l’obsolescence, et la dynamique du coût du SI dépend essentiellement de la baisse des prix unitaires.

Puis nous supposerons constant le volume du flux des nouveaux développements. Nous trouverons alors que le stock des applications tend vers un niveau limite S* (celui où le flux des nouveaux développements est exactement compensé par l’obsolescence des applications existantes). La dynamique avant d’atteindre le niveau S* dépend du niveau de départ S₀ : si S₀ est inférieur à S*, il y a croissance de S, et inversement S diminue si S₀ > S*. Une fois S* atteint, on retrouve la dynamique correspondant à un niveau constant de S examinée précédemment.

Les règles de gestion du SI “ en volume ” ont, sous l’hypothèse d’une baisse des coûts unitaires, un effet de compression sur le budget de l’informatique qui “ implose ” et tend à s’annuler à terme.

S_t constant

S_t = S

Le flux des nouvelles applications compense la perte due à l’obsolescence :

N_t = δS

Donc C_t = S(a_t + b_tδ), d’où :

ΔC/C = - k

Le coût total diminue au taux k à partir du coût initial C₀. Les autres coûts varient de même.

Voici l’évolution du budget informatique sous les hypothèses ci-dessus si l’on pose S = 1.

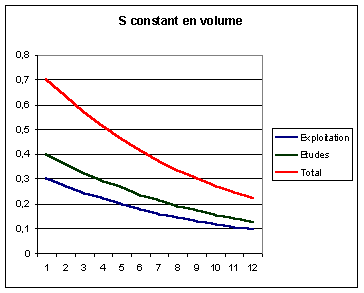
La décroissance du coût est due à l’hypothèse que nous avons faite sur le coefficient k. Si nous avions supposé k = 0 (pas de baisse des coûts unitaires), nous aurions trouvé des coûts constants.

N_t constant

N_t = N

S_t  = S_{t - 1}(1 - δ) + N

Il est utile d’introduire ici un résultat que nous allons utiliser à plusieurs reprises :

D’après ce résultat, si l’on pose S* = N / δ :

S_t  = S* + (S₀ - S*)(1 - δ) ^t

Lorsque t tend vers l’infini, S_t tend vers S*  ; selon que S₀ est supérieur ou inférieur à S*,  la série S_t converge vers S* en diminuant ou en augmentant. La convergence est d’autant plus rapide que δ est plus élevé.

Lorsque S_t est proche de sa valeur asymptotique S*, on retrouve la dynamique du cas précédent (où S est constant).

Voici l’évolution des coûts, en supposant N = 1 et S₀ = 0 :

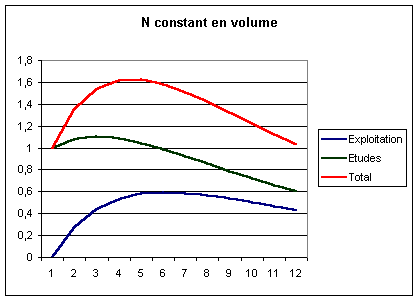
On observe que sous nos hypothèses le coût passe par un maximum avant de décroître : l’accumulation du stock S se fait ici au départ à un rythme plus rapide que k, ce qui entraîne un accroissement des dépenses d’exploitation ; puis, lorsque le stock approche le niveau asymptotique S*, on retrouve une dynamique semblable à celle observée précédemment.

L’allure de l’évolution aurait été bien sûr différente si nous avions choisi un niveau S₀ supérieur à S*.

Valeurs constantes

Coût constant des nouveaux développements

Supposons constant le budget consacré aux nouveaux développements :

b_tN_t = d

Dans ce cas,

N_t = (d/b)e^kt.

Le coût de maintenance et d’exploitation de l’année t est :

a_tS_t  = a_{t - 1}S_{t - 1}(1 - δ)e^{- k} + (ad/b)

D’après l’encadré 1, si l’on pose :

(a_tS_t)* = ad / b(δ + k), on obtient :

a_tS_t  = (a_tS_t)*+ [aS₀ - (a_tS_t)*](1 - δ) ^te^-kt

C_t tend vers la limite C* :

C* = d [1 + a / b(δ + k)]

Ainsi, si le coût des nouveaux développements est constant, on obtient à terme un budget informatique constant. Cette politique a donc un effet stabilisateur sur le coût de l’informatique. Les volumes, eux, croissent exponentiellement au rythme de la baisse des coûts unitaires.

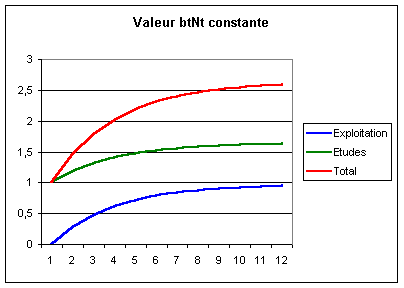
Part des nouveaux développements dans le budget constante

Supposons constante  la part des dépenses consacrée au développement de nouvelles applications dans le budget informatique :

c =  b_tN_t / C_t, avec 0 < c < 1.

NB : dans les simulations, nous supposerons que c = 50 %, proportion qui correspond au taux observé dans certaines directions informatiques.

C_t = a_tS_t/(1 - c)

Il en résulte que :

ΔC/C = ΔS/S - k

Par ailleurs,

N_t = acS_t / b(1 - c)

S_{t + 1} = S_t [1 - δ + ac/b(1 - c)], d’où

ΔS/S = ac/b(1 - c) - δ

ΔC/C = [ac/b(1 - c) - δ] - k

Il en résulte une évolution exponentielle du budget informatique. Son signe dépend de celui de [ac/b(1 - c) - δ] - k . Sous les hypothèses que nous avons retenues, l’exponentielle est croissante. Si l’on supposait la baisse des coûts plus rapide (par exemple k = 30 %), elle serait décroissante. Cette politique a donc un effet déstabilisateur sur le budget de l’informatique : il suivra une tendance exponentielle explosive ou implosive selon les coefficients.

Ainsi supposer le budget du développement constant a un effet stabilisateur ; mais supposer constante la part du développement dans le budget total a un effet déstabilisateur.

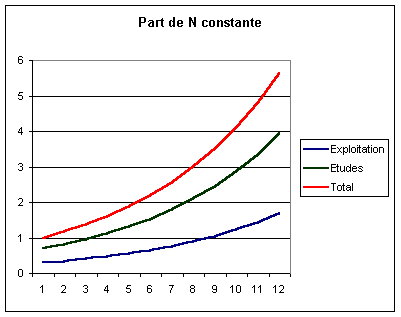
Supposons que k = δ = 0 (pas d’obsolescence, pas de décroissance des coûts) ; on aurait alors :

ΔC/C = ac/b(1 - c)

Dans ce cas, l’exponentielle est croissante puisque c < 1. Avec les paramètres retenus, on trouve ΔC/C = 50 %.

Avec δ = 20 %, on trouve ΔC/C = 30 %. L’évolution du coût est moins rapide s’il existe une obsolescence. Ce résultat semble paradoxal, puisque l’obsolescence est a priori coûteuse. Cependant elle a l’ « avantage » de réduire le stock en exploitation, donc les coûts d’exploitation. Le paradoxe est levé si l’on suppose le service rendu par l’informatique proportionnel au stock S ; le service rendu par unité de coût est :

P = S / C

l’évolution du service rendu par unité de coût, qui est un indicateur d’efficacité, est :

ΔP/P = ΔS/S - ΔC/C = k(1 + ΔS/S) = k [1 + ac/b(1 - c) - δ]

L’efficacité est d’autant plus forte que l’obsolescence est plus faible, ce qui est conforme à l’intuition.

Budget informatique total constant

Dans ce cas

C_t = C

N_t = (C - a_tS_t)/b_t

D’où :

a_{t + 1}S_{t + 1} = a_tS_t(1 - δ - a/b)(1 - k) + aC(1 - k)/b

Supposons que  1 - d - a/b > 0 ; comme 0 < (1 - δ - a/b)(1 - k) < 1, a_tS_t tend vers la valeur limite :

(a_tS_t)* = aC/[a + b(δ +k/(1 - k))],

et b_tN_t tend vers la valeur limite

(b_tN_t)* = C - (a_tS_t)*

Le rapport entre les coûts de développement et d’exploitation tend donc vers :

(b_tN_t)*/(a_tS_t)* = [δ +k/(1 - k)]b/a

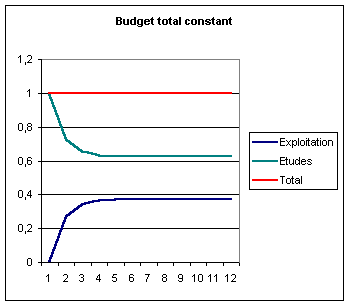
Il est intéressant d’examiner sur une variante ce que deviennent la dépense a_tS_t d’entretien du stock, et la dépense b_tN_t consacrée à l’accroissement du stock, si l’on suppose que la baisse des prix k et l’obsolescence d sont toutes deux nulles. On trouve alors l’évolution suivante :

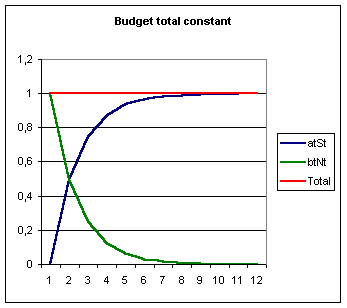
La règle “ budget constant ” conduit, si l’obsolescence est faible et la baisse de prix négligeable, à annuler les dépenses consacrées à l’innovation : la totalité du budget informatique étant à terme consacrée à la maintenance et à l’exploitation du stock existant, l’innovation est devenue impossible. La règle "budget constant", qui peut paraître a priori raisonnable et qui est en effet souvent appliquée par les entreprises, conduit à fixer les nouveaux développements à un niveau qui n'a aucune relation avec les besoins de l’entreprise.

Prise en compte des dépenses de la maîtrise d’ouvrage

Nous n’avons jusqu’à présent considéré que les dépenses proprement informatiques, car c’est sur elles que l’attention se focalise en général. Le coût d’un SI comprend aussi les dépenses de la maîtrise d’ouvrage. Elles se classent selon les rubriques suivantes :

-          dépenses de suivi du SI existant, proportionnelles au volume du SI existant ; leur montant pendant l’année t est αa_tS_t , où nous retiendrons α = 5 % ;

-          dépenses de mise en place : formation des utilisateurs, déploiement, conduite du changement ; on peut affecter ces dépenses à l’année qui suit l’investissement informatique,; leur montant pendant l’année t est βb_{t - 1}N_{t - 1}, où nous retiendrons β = 20 % ;

-          dépenses de suivi des réalisations : suivi du projet et recettes ; on peut affecter ces dépenses à l’année de réalisation ; leur montant pendant l’année t est γb_tN_t , où nous retiendrons γ = 10 % ;

-          dépenses de conception : expression des besoins, étude économique et sélection des projets, spécifications générales, validation des spécifications détaillées ; on peut affecter ces dépenses à l’année qui précède l’investissement informatique ; leur montant pendant l’année t est εb_{t + 1}N_{t + 1} , où nous retiendrons ε = 25 %.

Il en résulte que les dépenses de maîtrise d’ouvrage sont une fraction des dépenses consacrées à l’exploitation et à la maintenance du stock des applications existantes, plus une moyenne mobile des dépenses consacrées à la production des nouvelles applications :

A_t = αa_tS_t + βb_{t - 1}N_{t - 1} + γb_tN_t + εb_{t + 1}N_{t + 1} 

Lorsque le régime de croisière est atteint, les dépenses de la maîtrise d’ouvrage représentent dans les divers cas que nous avons considérés les pourcentages suivants par rapport aux dépenses informatiques :

-          S_t constant : 19,2 % ;

-          N_t constant : 19,2 % ;

-          b_tN_t constant : 16,2 % ;

-          part constante des nouveaux développements dans le budget informatique : 16,3 % ;

-          budget informatique constant : 16,5 %.

Conclusion

A l’issue de cet exercice, nous voyons que l’application de règles de gestion simples à l’informatique peut entraîner des effets imprévus :

-          volumes constants :

-          constance du volume du stock S_t des applications : les réalisations nouvelles ne font que compenser l’obsolescence ; le budget informatique décroît au rythme du prix des unités d’œuvre.

-          constance  du volume du flux N_t des nouveaux développements : le stock des applications tend vers une valeur limite S* ; après quoi le budget informatique décroît au rythme du prix des unités d’œuvre.

-          valeurs constantes :

-          constance  de la valeur du flux b_tN_t des nouveaux développements : le budget informatique tend vers une limite C*. Cette politique a donc un effet stabilisateur – toute la question étant de savoir si la dépense C* est optimale ou non.

-          part constante des nouveaux développements dans le budget : le budget informatique a une évolution exponentielle, explosive ou implosive selon les valeurs des coefficients. Cette politique est donc déstabilisante.

-          budget total constant : si le budget informatique est constant, les parts consacrées aux nouveaux développement et à la maintenance tendent toutes deux à se stabiliser. Cette politique est par nature stabilisatrice en termes budgétaires, mais elle peut avoir des effets extrêmes selon les coefficients (il peut par exemple arriver que les dépenses consacrées aux nouveaux développements soient totalement laminées). On retrouve donc ici la même question que ci-dessus : il faudrait pouvoir définir le budget informatique optimal de l’entreprise.

Nos simulations ont exploré les conséquences de règles de gestion appliquées de façon mécanique. Dans la pratique, une entreprise saura modifier ses règles pour éviter la catastrophe : derrière la succession des règles se profile la recherche implicite d’un optimum.