A la recherche du taux d’informatisation optimal

2 février 2002

Nous avons dans une première fiche examiné des profils d’évolution résultant de principes de gestion que l’on rencontre dans la pratique, mais qui ne représentent qu’une approximation imprécise de ce que peut être la dynamique optimale du système d’information de l’entreprise.

Nous allons tenter de donner un contenu à cette dernière expression en utilisant des notations analogues à celle de la fiche précédente et en supposant :

-          que l’entreprise cherche à maximiser la valeur actualisée de son profit[1].

-          que la fonction de production de l’entreprise est une fonction de Cobb-Douglas à rendement constant :

(1) Y = F(S, L) = S^μ L^ν avec μ + ν = 1,

où S est la taille du système d’information (c’est un stock que l’on peut mesurer par le nombre de lignes de code source, le nombre de points de fonction ou par toute unité analogue, peu importe ici) et L le volume du travail employé par l’entreprise. Nous supposons que le prix p auquel Y est vendu sur le marché est unitaire. Le salaire annuel est w et  le volume du facteur travail L croît au rythme annuel τ que nous supposons exogène.

On peut bien sûr utiliser d’autres spécifications de la fonction de production (notamment la fonction de production à facteurs complémentaires). Cependant la fonction de Cobb-Douglas est celle que les économistes utilisent le plus souvent parce qu’elle est la plus simple, la plus banale qu’il soit possible d’imaginer – et aussi parce que l’on peut démontrer que si les entreprises d’un même secteur concurrentiel ont chacune une fonction de production à facteurs complémentaires, le jeu de la concurrence et de la libre entrée fait que le secteur lui-même, considéré comme un ensemble, aura pour fonction de production une Cobb-Douglas à rendement constant[2].

Lorsque l‘économiste utilise une fonction de production, il suppose implicitement résolus les problèmes d’efficacité que pose la mise en œuvre des facteurs : Y sera la production maximale qu’il est possible d’obtenir en utilisant les quantités S et L des facteurs (s’agissant du système d’information, on suppose donc que les méthodes utilisées pour le construire et l’exploiter sont les meilleures, qu’il s’agisse de la qualité et du contrôle des logiciels ou de la maintenance etc.) Il reste alors à déterminer la stratégie d’informatisation la plus efficace compte tenu du coût des facteurs et des buts de l’entreprise, cette stratégie se réduisant au choix de la série chronologique S_t.

Si l’on note N_t le volume des nouveaux développements réalisés lors de l’année t et δ le taux d’obsolescence du SI existant, le volume du SI en exploitation l’année t est :

(2) S_t  = S_{t – 1} (1 - δ) + N_t

L’évolution de S_t est donc connue si l’on connaît le stock initial S₀ et la série des N_t.

Le coût du système d’information est :

(3) C_t  = (aS_t  + bN_t)e^-kt

(Nous retenons ici une expression simplifiée du coût, la prise en compte des dépenses de maîtrise d’ouvrage pouvant se faire simplement).

Nous supposons que l’entreprise cherche à maximiser la valeur actualisée d’une fonction d’utilité selon le taux d’actualisation exogène r :

(4) W = ∫(Y_t – wL_t - C_t)^ξe^-rt dt , avec ξ ≤ 1.

Si ξ = 1, W est la valeur actualisée du profit. Si ξ < 1, l’entreprise accorde d’autant plus d’importance au profit que celui-ci est plus bas, ce qui correspond à un comportement très répandu.

Le problème du niveau optimal d’informatisation peut être analysé, selon les méthodes de la programmation dynamique, en termes de « variables d’état », « variables de contrôle », « équations du mouvement », « état initial », « état final » et « fonction objectif ».

Associons à toutes les quantités (S, N etc.) une quantité par personne que nous représenterons par une lettre minuscule (s = S/L, n = N/L, etc.). Notons τ le taux de croissance de l’effectif L. 

La fonction de production s’écrit alors :

(5) y = F(S, L)/L = f(s) = s^μ

La variable d’état est alors le « taux d’informatisation par personne » s.

Supposons d’abord que k = 0 (le prix des unités d’œuvre est constant). Dans ce cas, le coût de l’informatique par personne est :

(6) c_t  = as_t  + bn_t

La variation du stock informatique par personne entre l’année t et l’année t + 1 est égale au volume des nouveaux développements par personne, moins la perte due à l’obsolescence, moins l’effet de la croissance du nombre des personnes :

(7) ds_t/dt = n_t – (δ + τ)s_t

Le profit par personne l’année t est, en notant w le coût d’une personne :

(8) π_t = y_t – w - c_t

en éliminant n_t entre ces relations, on obtient l’équation du mouvement :

(9) ds/dt = [f(s) - w – π]/b – λs, avec λ = a/b + δ + τ,

L’état initial est caractérisé par le niveau s₀ du taux d’informatisation à l’instant initial t₀. Du point de vue de l’entreprise, la variable de contrôle est le profit par personne π ; le problème est de choisir un sentier π(t) sur l’intervalle (t₀, t₁).

Toute trajectoire π satisfaisant l’équation du mouvement et la condition 0 ≤ π ≤ f(s) - as - w  étant possible, le problème est de choisir parmi les trajectoires possibles celle qui maximise la fonction objectif.

On trouvera en annexe le raisonnement qui conduit au taux d’informatisation optimal s* :

(10) s* = {µ/[a + b(r + δ + τ(1 – ξ))]}^{1/(1 - µ)}

les autres valeurs stationnaires s’en déduisent :

(11) y* = s*^μ ; n* = (δ + τ)s* ; c* = s*[a + b(δ + τ)].

Le profit par personne est π* tel que :

(12) π* = f(s*) - c* - w

On appelle l’équilibre en (s*, π*) “ sentier de croissance équilibré ”. Le long de ce sentier, la production totale Y, le profit total et le stock total S croissent tous au taux τ du nombre L_t des personnes.

Ainsi le taux optimal d’informatisation existe et il est unique. L’entreprise qui respecte ce taux maximise l’efficacité de son système d’information. Si elle s’en écarte, elle est soit sous-informatisée, soit sur-informatisée.

Évidemment l’expression (10) résulte des hypothèses concernant la fonction de production et le coût du SI. Elle ne saurait être appliquée sans précautions à une entreprise concrète, pour laquelle il est toujours difficile de spécifier la fonction de production et la fonction de coût. Elle fournit toutefois des enseignements intéressants :

-          comme il existe un taux d’informatisation optimal, une politique qui consisterait à supprimer l’informatisation, ou à l’accroître indéfiniment, n’est pas efficace.

-          le taux d’informatisation est fonction décroissante du prix a de la maintenance, du prix b des développements, du taux d’obsolescence δ, et aussi (si ξ < 1) du taux de croissance des effectifs τ.

-          si ξ = 1, c’est-à-dire si la fonction objectif de l’entreprise est le profit actualisé, le taux d’informatisation ne dépend pas de la vitesse τ de la croissance des effectifs.

-          comme en général [r + δ + τ(1 – ξ)] < 1, le taux d’informatisation optimal est plus sensible au coût de la maintenance qu’au coût du développement. Le coût de la maintenance est donc celui auquel il convient d’être le plus attentif (cette indication est généralement admise, mais on en tire rarement les conséquences tant l’attention est accaparée par les développements).

-          le taux d’informatisation optimal ne dépend pas du taux de salaire w (mais l’entreprise ne peut exister que si le niveau de w lui permet de dégager un résultat positif).

Si les valeurs initiales et finales s₀ et s₁ de s sont égales à s*, la trajectoire optimale est celle qui maintient continûment le taux d’informatisation à son niveau s*.  Si s₀ et/ou s₁ sont différents de s*, le « théorème du péage[3] » nous indique que le taux d’optimisation suivra une trajectoire qui, à partir de s₀, rejoindra rapidement le niveau s* dont elle ne s’écartera que peu de temps avant de rejoindre le niveau s₁. Les simulations fournies dans la deuxième partie de cette fiche illustrent ce phénomène. 

Simulations numériques[4]

On prend pour paramètres les valeurs s_t et on maximise la valeur actualisée de l’utilité calculée sur l’ensemble de la période considérée.

Prenons les valeurs suivantes des coefficients :

µ = 0,5 ; d = 0,1 ; r  = 0,1 ; x = 0,8 ; a = 0,5 ; b = 1 ; τ = 0 ; w = 0,2.

Si k = 0, on trouve s* = 0,5102. Supposons que les valeurs initiales et finales sont s₀ = 0,3 et s₁ = 0,7. La simulation sur 20 ans fournit la série s_t optimale suivante, dont l’allure fait bien apparaître le phénomène du péage : 

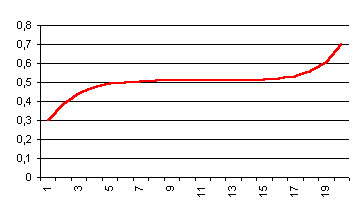
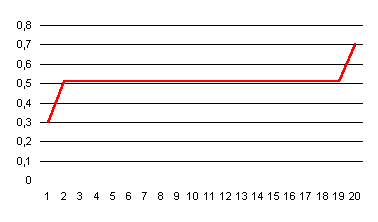
Si l’on suppose que ξ = 1 (la fonction objectif est le profit actualisé), on trouve que le phénomène du péage est brutal : le taux d’informatisation rejoint la valeur s* dès l’année 1 et ne s’en écarte que la dernière année :

La simulation numérique permet de traiter des problèmes qui n’ont pas de solution analytique. Supposons par exemple que le coût unitaire du système d’information diminue en posant k = 10 %. Si nous conservons les mêmes valeurs de s₀ et s₁, nous obtenons l’évolution suivante de s_t :

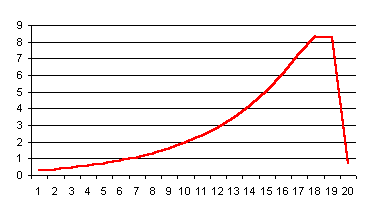
Il est intéressant d’examiner la part du budget informatique dans la valeur de la production ; on trouve alors un résultat important : cette part est constante, sauf vers la fin de la période :

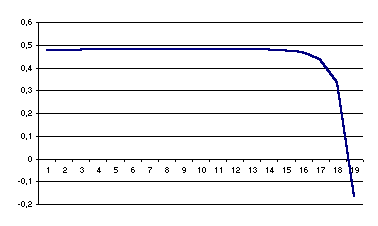
Ce résultat évoque un phénomène de péage, la variable d’état étant alors non le taux d’informatisation mesuré selon le volume par personne s_t mais la part du budget du SI dans le chiffre d’affaires. On peut, par tâtonnement, trouver la trajectoire optimale qui maintient ce rapport  à peu près constant (il est exactement constant si ξ = 1). On voit alors que le taux d’informatisation optimal s_t suit une trajectoire exponentielle.

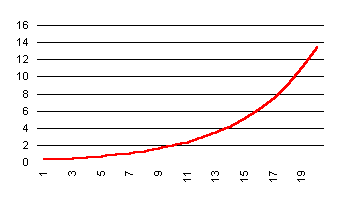
La simulation numérique nous apporte donc, outre une visualisation du phénomène du péage, les constats suivants :

-          le phénomène du péage est d’autant plus brutal que ξ est plus élevé (c’est-à-dire que l’entreprise raisonne en terme de profit actualisé) ;

-          lorsque le coût du SI baisse de façon exponentielle (k > 0) la variable d’état qu’il convient de contrôler est non le taux d’informatisation s_t, mais le rapport c_t/y_t entre le coût du SI et le chiffre d’affaire, et le taux d’informatisation optimal croît de façon exponentielle.

Bibliographie

Jean-Louis Peaucelle, Informatique rentable et mesure des gains, Hermès 1997

Peter G. W. Keen, Shaping the Future, Business Design through information technology, Harvard Business School Press 1993

Jacques Printz, Puissance et limites des systèmes informatisés, Hermès 1998

Michael D. Intriligator, Mathematical Optimization and Economic Theory,  Prentice-Hall 1971