Rentabilité d'un ensemble de projets

13 janvier 2003

(Voir « Faire évoluer le SI ») 

A tout projet on peut associer l’anticipation d’un flux de trésorerie disponible [1] ; cette anticipation comporte évidemment une part d’incertitude dont il convient de tenir compte. 

Le flux de trésorerie disponible F_t  est l'écart annuel entre les recettes et les dépenses associées au projet, y compris lors de la phase d'investissement initiale. Si l'on considère par exemple un projet qui demande la dépense d'investissement K l'année 0 puis qui rapporte les années suivantes le résultat brut R sans limitation de durée, la série F_t s'écrira : F₀= - K, F₁ = R, F₂ = R, F₃ = R, etc.

On calcule, à partir du flux de trésorerie, deux indicateurs synthétiques : la « valeur actuelle nette » (VAN) et le « taux de rentabilité interne » (TRI) du projet.

Valeur actuelle nette

La VAN est la somme actualisée de la variation de trésorerie disponible ; le taux d’actualisation à retenir est égal au taux d’intérêt du marché monétaire augmenté d’une prime de risque pour tenir compte de l’incertitude (le futur compte d’autant moins qu’il est plus éloigné) :

r = i + π

Le choix de la prime de risque à utiliser dans le calcul, ainsi que du taux d’intérêt à considérer, relève de la direction générale s'appuyant sur l’expertise de la direction financière ; il doit être révisé chaque année. La VAN a alors, en sommant sur la durée de vie du projet :

VAN = Σ F_t /(1 + r)^t

Taux de rentabilité interne

Le TRI est la valeur du taux d’actualisation qui annule la VAN ; il est solution de l’équation :

Σ F_t /(1 + TRI)^t = 0

On doit rejeter immédiatement tout projet dont le TRI est inférieur au taux d'actualisation r, car sa VAN est négative. 

Examen d’un projet simple

Nous appellerons « projet simple » un projet qui coûte en année 0 un montant K et qui rapporte pendant chacune des années suivantes le résultat brut R, la durée de vie du projet étant infinie.

Dans ce cas on trouve :

VAN = R/r – K

TRI = R/K

La deuxième équation permet de comprendre ce qu'est le TRI : si le projet coûte K la première année, puis rapporte R chacune des années suivantes, le projet est analogue à un « placement » dont le taux d'intérêt serait égal à son TRI. 

« Projet simple » équivalent à un projet

Considérons un projet donc nous connaissons la VAN et le TRI. On peut associer à ce projet un « projet simple » qui aura la même VAN et le même TRI, et qui lui sera donc équivalent à cet égard. Les valeurs de K et de R du « projet simple » s’obtiennent en inversant la relation ci-dessus. On trouve :

K = r VAN / (TRI – r)

R = r VAN TRI / (TRI - r)

Classement des projets

A chaque projet nous associons le « projet simple » correspondant. Dans le plan (K, R) le projet sera représenté par un point P, la pente du segment OP étant égale à son TRI :

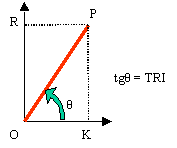
Classons les projets dans l’ordre des TRI décroissants en enchaînant l’un à l’autre des segments de droite représentant chacun un projet ; on obtient une courbe polygonale dont la concavité est tournée vers le bas (dessinée ici en bleu) :

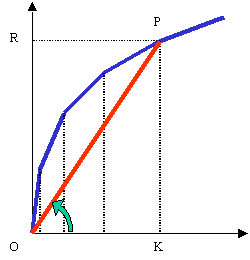
Supposons que l’on décide de réaliser les quatre projets dont le TRI est le plus élevé. La dépense totale sera la somme K des coûts de ces projets, le résultat brut total sera la somme des résultats bruts ; la rentabilité de l’investissement ainsi réalisé est le rapport de ces deux totaux.

Remarques et précautions

1) Le budget annuel nécessaire à la réalisation de ces projets ne sera pas exactement égal à la somme K, puisque nous avons considéré non les projets eux-mêmes, mais les « projets simples » qui leur sont équivalents. Néanmoins cette somme donne la mesure de l’effort d’investissement nécessaire.

2) Les évaluations qui fondent le classement sont entachées d’incertitude et par ailleurs le choix du taux d’actualisation r comporte une part d’arbitraire ; toutefois elles résument les informations que l’entreprise détient au moment de la décision.

3) Le raisonnement ci-dessus considère des projets dont le niveau de risque est analogue ; si un projet comporte un risque beaucoup plus élevé que les autres, il faudra en général le rejeter ; si le risque est beaucoup plus faible, il faudra l'examiner à part et éventuellement le faire passer en priorité. 

4) Le raisonnement ci-dessus suppose que l'on a déjà considéré les synergies entre projets. Si la synergie entre les projets P₁ et P₂ est élevée (en les lançant tous deux, on obtient par exemple un résultat fortement supérieur à R₁ + R₂), il faut les regrouper en un même projet ; si la synergie est fortement négative (ils utilisent tous deux une même ressource rare, ou bien leur réalisation conjointe brouillerait le positionnement de l'entreprise), il ne faut retenir que l'un des deux. Ces décisions doivent avoir été prises avant la présentation de la liste des projets au directeur général. 

5) Le calcul de rentabilité ignore les aspects d’un projet qui sont difficiles à « chiffrer ». C’est pourquoi le classement par ordre de rentabilité décroissante doit être soumis à l’arbitrage du directeur général. Il sera libre, s’il le juge utile, de modifier l’ordre des priorités, de « tuer » tel projet que l’on avait jugé rentable, de « repêcher » tel autre projet qui avait été mal classé. Il faut que les experts acceptent la valeur ajoutée qu’apporte le dirigeant, qui est le mieux placé pour avoir une vue d'ensemble des enjeux stratégiques (voir « Expertise et décision »).

6) Certains estiment que l’importance d’un projet se mesure non à son TRI, mais à sa VAN : ils classent donc les projets non dans l’ordre des TRI décroissants, mais dans l’ordre des VAN décroissantes. Cependant la VAN, étant fonction croissante à la fois du TRI et de la taille du projet, résulte du jeu conjugué de deux critères. Nous préférons pour notre part laisser le directeur général apprécier l'importance relative des projets et lui présenter un classement qui, fondé sur le seul critère du TRI, maximise la rentabilité (anticipée) de l'investissement.