|
La statistique utilisée pour la manipulation
15 septembre 2001
(cf. "les institutions contre
l'intelligence")
(Contribution à La Manipulation à la française,
sous la direction de Philippe Ricalens, Economica 2003)
L’obscure clarté qui tombe des nombres
Observez ce qui se passe dans votre tête lorsqu’un conférencier affiche des
tableaux de nombres ou cite des pourcentages. Pour que vous puissiez interpréter
ces statistiques, il faudrait qu’elles fussent présentés de façon sélective,
sobre, intelligente, honnête en un mot. Mais parfois ce n'est pas le but du
conférencier. Il s'agit pour lui non d'être compris mais de célébrer la liturgie
du nombre, faite pour impressionner et endormir l’esprit critique. Personne
n'osera lever le doigt et dire " je n'y comprends rien " : chacun feignant de
s'y retrouver, les rieurs seraient pour le conférencier.
Rédiger une étude statistique claire, apportant réellement une information,
c’est un exercice dont la difficulté est d’autant plus grande, mais d’autant
moins apparente, que le résultat sera plus simple. Michel-Louis Lévy, lorsqu’il
était rédacteur en chef de " Populations et société ", publiait en quatre pages
d’excellentes synthèses. Mais comme elles étaient simples peu de personnes
percevaient la qualité de son travail. L’admiration va aux travaux
incompréhensibles d’apparence sérieuse. Il est tentant pour le statisticien de
céder à la facilité, d’où l’avalanche de publications illisibles.
Quand la statistique est muette
La production statistique ne peut commencer que lorsqu'on a établi des
nomenclatures pour définir et classer les objets observés. Or construire une
nomenclature est une longue affaire. Il existe des époques où l'on n’en dispose
pas encore. La statistique est alors muette. Si on la fait parler de force,
c’est pour tromper ou impressionner : le nombre ne peut alors apporter que la
confusion. Mais le mépris accablera celui qui met en doute sa pertinence. " Vous
êtes un philosophe " (et non un économiste ou un manager), ou encore " vous êtes
un sociologue ", lui dira-t-on en ricanant (Mais
quiconque associe une connotation péjorative à un terme comme
"philosophe", "sociologue", "technicien", "ingénieur" etc. s’exclut ipso
facto de la conversation sérieuse). Le voilà
expulsé de la corporation des gens " sérieux " qui cultivent ce que Feynman
appelait la " science prétentieuse ".
La statistique est ainsi aujourd’hui muette sur la " nouvelle économie ". Les
concepts ne sont pas définis. Les séries chronologiques sont trop courtes pour
étalonner les modèles. On peut mesurer la valeur des échanges marchands mais il
est impossible de distinguer dans son évolution l’effet volume et l’effet prix
en raison des changements rapides de la qualité des produits. Chaque pays
évaluant à sa façon les données macro-économiques (et notamment le partage
volume - prix), la comparaison internationale est pratiquement impossible.
Certaines innovations ne sont pas prises en compte : ainsi le téléphone mobile
n'est pas représenté dans l'indice du prix de la consommation des ménages en
France, alors que pratiquement la moitié des personnes sont équipées. Il ne faut
pas en vouloir aux statisticiens car le problème est redoutable (comment
construire un indice qui recouvre l'évolution de tarifs aussi divers ?). Les
statistiques étant en retard par rapport à l’économie, il en résulte de délicats
problèmes d’interprétation (Le paradoxe de Solow " You
can see the computer age everywhere these days, except in the productivity
statistics " (1982) est à double sens. Cette phrase peut signifier que les
ordinateurs ne contribuent pas à la productivité, mais aussi que les
statistiques de productivité sont inexactes).
Cette situation n'est pas sans précédent. Dans la première moitié du XIXème
siècle, l'industrie était toute nouvelle et les concepts pour la décrire
n'existaient pas (cf. Bernard Guibert,
Jean Laganier et Michel Volle, " Essai
sur les nomenclatures industrielles ", Economie et Statistique, n° 20
février 1971). Qu'ont fait les statisticiens de
l’époque ? des monographies. Ils n'ont pas calculé des totaux ou des
moyennes, car les marchés étant loin du point d'équilibre un total aurait
recouvert des quantités hétérogènes ; mais ils ont fourni sur chaque
établissement les informations permettant de constater ses performances. La
monographie, c'est le préliminaire de la statistique, l’étape où l'on dégage les
concepts qui fonderont ensuite nomenclatures, enquêtes et calculs.
Nous en sommes au même point avec les nouvelles technologies. Utiliser ici la
statistique, la macro-économie, les comparaisons internationales, l'économétrie,
c'est se croire plus avancés que nous ne le sommes. Cela ne signifie pas que
l'on doive renoncer aux cadres théoriques que fournit la pensée économique, mais
qu’il faut se garder de plaquer sur une réalité nouvelle un cadre conceptuel
hérité d'autres époques (Jean Tirole
et Josh Lerner ont avec raison retenu l’approche monographique dans " The
Simple Economics of Open Source " (17 janvier 2001) : " Reflecting the early stage of
the field’s development, we do not seek to develop new theoretical frameworks or
to statistically analyze large samples. Rather, we focus on four " mini-cases "
of particular projects: Apache, Linux, Perl, and Sendmail ").
Lors d'un séminaire sur l'économie de la connaissance, un " économiste " a
proposé de se limiter à l'examen des échanges marchands " parce qu'ils sont
observables et que nous avons des données ". N'êtes-vous pas en train de
chercher votre clé sous le réverbère, lui ai-je demandé ? que faites-vous de ce
qui se passe dans les entreprises en matière de " groupware ", " knowledge
management ", " datawarehouse ", " datamining ", système d'aide à la décision
etc.? rien de tout cela n'est marchand puisque cela se passe dans
l'entreprise, mais n’est-ce pas l'essentiel de ce qui se fait en économie de la
connaissance ? " Nenni, me répondit-il en anglais, vous êtes un philosophe, je
ne peux travailler que si j'ai des données quantitatives ".
Les grands économistes ne sont pas de grands économètres. Il y a peu de
statistiques dans les œuvres de Smith, Marshall et Hicks. Cela ne veut pas dire
qu’ils étaient indifférents aux faits. Seulement ils n’éprouvaient pas le
besoin, pour en imposer, d'abrutir leur lecteur par des calculs impertinents.
Certes le recours au quantitatif est parfois indispensable au raisonnement.
Si par exemple une entreprise augmente son prix de vente, elle fera un profit
unitaire plus élevé mais vendra moins d’unités. Il faut connaître l’élasticité
de la demande qui lui est adressée pour savoir s’il en résultera une hausse ou
une baisse de son profit. Le raisonnement qualitatif ne peut ici aboutir que
s’il passe par une étape quantitative. Mais il y a loin entre la débauche de
tableaux de nombres et d’économétrie dont on nous accable et l’usage sobre,
pondéré, respectueux du quantitatif.
Orientation du regard
L’observable statistique n’est pas borné seulement par le délai d’adaptation
à l’évolution économique. L’investissement nécessaire pour établir les
nomenclatures est sélectif. La statistique a des pudeurs maintenues par de
robustes rapports de force institutionnels (cf
Michel Volle, Rapport
Général sur l'évolution à moyen terme de l'appareil statistique français,
rapport au Conseil National de l'Information Statistique, 1989).
On connaît mal les revenus non salariaux et les patrimoines, sur lesquels on ne
dispose que de sources fiscales polluées par la fraude. Il serait techniquement
possible, bien que difficile, d'organiser une observation plus rigoureuse : les
moyens de réaliser ces travaux n'ont pas été mis en place en raison de blocages
culturels et politiques (L'administration
fiscale, qui a une mission répressive, possède des pouvoirs d'investigation plus
étendus que la statistique, qui pourtant ne considère l'information individuelle
que comme une étape dans l'élaboration des résultats globaux et garantit le
secret.).
On ignore comment sont réparties les primes des fonctionnaires. Les aides de
l'Etat aux entreprises sont moins bien connues que les crédits accordés par les
banques. Le fonctionnement des groupes d'entreprise, notamment les échanges
entre la partie nationale et la partie étrangère des multinationales, sont mal
connus. La face interne de l'entreprise (organisation du travail, formation
professionnelle " sur le tas " et qualifications de fait, carrières
individuelles, structures de décision) n’est pas observée par l'appareil
statistique : le lieu de travail, où chacun passe l'essentiel de son temps, est
considéré comme l'affaire de l'entreprise, non celle du citoyen.
L'orientation de l'appareil statistique, le choix de ce qui sera observé et
de ce qui ne le sera pas, ne sont pas innocents. Ce choix comporte plusieurs
étapes : le statisticien propose, de nombreuses instances donnent leurs avis,
finalement le Budget décide. Or celui qui tient les cordons de la bourse peut,
sous prétexte d’éviter le gaspillage, permettre ceci et empêcher cela. Il est
possible que, parmi les raisons qui poussent un responsable à juger telle
enquête nécessaire et telle autre inutile, figure un reflet de son idéologie
personnelle et de celle de son milieu social. Le statisticien public, lui,
travaille selon les crédits qu'il a reçus ; en bon fonctionnaire il fonctionne,
même s'il pense confusément que l'on aurait dû faire autre chose que ce qui a
été décidé.
Orientation de la publication
Tout pouvoir politique, s'il a une position de principe favorable à long
terme au développement de l'information statistique, demande qu'à court terme on
lui épargne les embarras que provoque la publication de chiffres gênants.
Certaines statistiques ont une résonance politique : indice des prix, niveau du
chômage, solde de la balance commerciale, pouvoir d'achat des agriculteurs, etc.
Les interventions prennent diverses formes : retouches apportées à un
commentaire (le mot " crise " a longtemps été mal vu), retard de quelques jours
apporté à une publication (ou accélération si la publication est favorable),
écho sélectif donné par les médias. Les truquages portent sur le commentaire, la
présentation, l'explication ; je n’ai pas connaissance d'un cas où un
statisticien aurait " truqué les chiffres ", mais il est arrivé qu'un ministre
utilise la voie administrative pour obtenir qu'un indicateur aille dans le bon
sens : ainsi la gestion de l'ANPE fut opportunément modifiée avant les élections
de 1978 ; ainsi le ministre des Finances est intervenu en 1976 auprès d'EDF pour
limiter la hausse de l'indice des prix.
" Volontarisme " de la prévision
Outre les difficultés techniques de l’observation, les statisticiens
rencontrent le " volontarisme " du pouvoir politique. Celui-ci se fait fort
d'obtenir, par une action " volontaire " que tel ou tel indicateur économique
important - la croissance du P.I.B., la hausse des prix, la balance commerciale,
le niveau du chômage - s'établisse dans le futur à un niveau déterminé. Ce
niveau devient alors dans les calculs une norme que les techniciens doivent
respecter et à partir de laquelle ils doivent déterminer les autres variables.
On pourrait comprendre que le pouvoir demandât de fixer à un niveau déterminé
les indicateurs sur lesquels il a la volonté réelle et les moyens d'agir ; mais,
confondant technique et action psychologique, il tend à fixer de façon
volontaire la plupart des indicateurs politiquement importants, même ceux qui
sont en pratique hors de sa portée, en les situant à des niveaux grossièrement
invraisemblables. Les techniciens, parfaitement conscients, font morosement
tourner leurs équations. Ils savent que lorsque le pouvoir aura été démenti par
les faits on les accusera d'incompétence ; ils savent que les techniciens des
autres services d'études économiques se plaignent du manque de vraisemblance des
budgets économiques. La moitié environ des fonctionnaires
de la direction de la Prévision ont signé en 1977 une lettre envoyée au Premier
ministre par les sections syndicales C.G.T. et C.F.D.T. ; cette lettre contient
le passage suivant : " Taux d'inflation, chômage, déficit des finances publiques
et commerce extérieur nous sont imposés par les instances gouvernementales,
quitte à ce que l'on se retourne contre les experts qui se sont trompés " (Le
Monde, 13 octobre 1977).
Les excès du volontarisme sautent aux yeux lorsqu'on confronte prévisions et
réalisations. Une étude réalisée par les techniciens de la prévision
(J. Boulle, J. Bouysset, H. Perker,
"Les budgets économiques et leur réalisation",
S.E.F. collection orange n° 18 1975) a montré que
les prévisions de la croissance annuelle des prix à la consommation ont été
systématiquement optimistes : l'erreur moyenne était de - 1,6 %.
Présentations fallacieuses
" Comment mentir avec des statistiques " est le titre d'un livre plein
d'humour (Darrell Huff, How to Lie
with Statistics, Norton 1954). Voici quelques
astuces simples mais efficaces.
Inverser la tendance
Malgré ses ondulations, il est clair que la courbe en traits fins ci-dessous
a tendance à descendre :
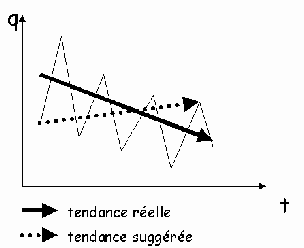
Voulez-vous faire croire qu'elle monte ? Il suffit de prendre un point bas au
début, un point haut vers la fin, puis de dire " la croissance entre janvier et
décembre a été de x % ". Ce sera vrai et cela vous permettra de donner une
impression fausse.
Effet d’échelle
Si vous superposez sur un même graphique deux courbes ayant des échelles
différentes il se peut que la série qui croît le plus vite semble moins pentue
que l’autre. Vous pourrez ainsi égarer le jugement du lecteur.
Par exemple sur le graphique ci-dessous, l’échelle de gauche est relative à
la série 2, l’échelle de droite à la série 1. La série 2 croît plus vite que la
série 1, mais c’est l’inverse qui apparaît.
Pour éviter cette erreur, il aurait fallu caler la valeur
zéro de chaque variable sur une même ligne virtuelle située sous le graphique.
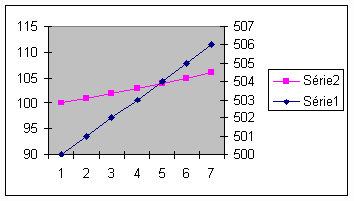
Déguiser les rythmes de croissance
Si on représente graphiquement une série qui croît rapidement, on ne verra
sur le graphique qu’une exponentielle peu lisible. Pour faire apparaître les
changements de tendance, il faut soit utiliser une échelle logarithmique (une
croissance à taux constant est alors représentée par un segment de droite), soit
représenter l’évolution du taux de croissance.
Pour le lecteur non averti la relation entre les trois représentations
(évolution de la donnée, de son logarithme, de son taux de croissance) n’a rien
d’évident. Il sera possible de l’induire en erreur en choisissant, selon le cas,
la présentation qui oriente son intuition vers la conclusion voulue.
Recours saisonnier à la CVS
Il est parfois opportun de retenir, selon la saison, la série brute ou la
série corrigée des variations saisonnières (CVS). Durant la première moitié de
l'année, la série brute du chômage a coutume de baisser : on citera alors
volontiers les chiffres bruts. Par contre, à partir de septembre, l'afflux des
jeunes fait gonfler les données brutes plus vite que les données CVS : ce sont
ces dernières que l’on citera. L’utilisation de la correction des variations
saisonnières présente ainsi un caractère saisonnier.
Erreurs classiques
Les dirigeants de certaines entreprises ont pris l’habitude d’utiliser des
méthodes erronées qui donnent une forme " évidente " à des résultats fallacieux.
Les experts sont donc parfois contraints de passer par ces méthodes et ils ont
fort à faire pour éviter aux dirigeants les erreurs auxquelles elles conduisent.
Certains peuvent tirer parti de ces mauvaises habitudes pour manipuler les
dirigeants et faire passer les décisions qui leur conviennent.
Estimation de la tendance par comparaison à l’année passée
Certains aiment, pour évaluer une tendance, à comparer le nombre du dernier
mois connu avec celui du mois correspondant de l’année précédente. C’est ce que
l’on appelle le " R/R " (" réalisé sur réalisé ").
Cette méthode comporte des variantes : on peut l’appliquer non à la valeur du
mois, mais à la valeur cumulée depuis le début de l’année, à la somme sur les
douze derniers mois, etc. : l’imagination des calculateurs n’a pas de bornes et
les ordinateurs sont dociles. Certains calculateurs
programment diverses méthodes plutôt que de choisir la méthode convenable.
Jean-Paul Benzécri diagnostiquait alors le " syndrome du singe dactylographe ".
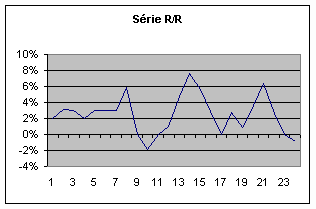
Certains croient que cette méthode permet de corriger les effets saisonniers.
Cependant elle est fallacieuse, même si la courbe semble facile à lire. Obtenue
en divisant les valeurs récentes par celles de l’année d’avant, elle superpose
de façon inextricable les effets de deux conjonctures. Une même courbe R/R peut
ainsi recouvrir des évolutions différentes selon les valeurs observées lors de
la première année :
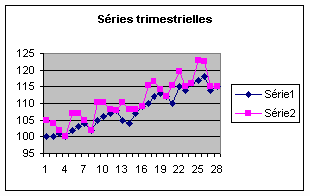
Le caractère fallacieux de cette méthode n’empêche pas qu’elle plaise à ceux
qui jugent la série R/R " plus simple à calculer " (c’est vrai) et " plus facile
à interpréter " (c’est faux) qu’une série CVS.
Comparer réalisation et prévision
Vers septembre de l’année n - 1, le contrôle de gestion de l’entreprise
établit les comptes prévisionnels de l’année n, fondés sur une " prévision " de
chiffre d’affaires et de dépense. Par la suite, en cours d’année, on calcule des
ratios " R/P " (" réalisé sur prévu "). On pensera que tout va bien si ces
ratios sont convenables.
Or les prévisions initiales sont inévitablement établies quelque peu " au
pif ". Si l’entreprise se contente pour évaluer sa situation économique de la
comparaison entre les réalisations et de telles " prévisions ", elle se prive
des enseignements que lui apporterait l’examen attentif de la conjoncture, du
marché etc.
Utiliser une courbe au lieu d’un histogramme
Quand on veut comparer des données relatives à des régions, à des produits
etc. il vaut mieux utiliser un histogramme qu’une courbe : comme la position des
points représentants les diverses régions ou produits sur l’axe des abscisses
est arbitraire, la pente que fait apparaître une courbe n’a aucun sens. J’ai
pourtant vu commenter la pente d’une courbe sur un graphique représentant des
chiffres d’affaires par région.
Un " fromage " hors de saison
Les " fromages " sont faits pour visualiser des répartitions en pourcentage à
l’intérieur d’une quantité (par exemple, le chiffres d’affaire par produit, la
population par région, etc.). Il ne faut pas les utiliser pour visualiser des
ratios (consommation par tête dans diverses régions, prix unitaire par produit),
qui seront mieux représentés par un histogramme.
Quelques erreurs sophistiquées
L’erreur peut être cachée par des méthodes élaborées : elle est alors
difficile à détecter car la technicité la protège en l’entourant comme un nuage
d’encre. Il m’est arrivé de décortiquer le progiciel dont se servait une banque
pour évaluer des provisions pour risque : heureusement, nous disposions du code
source. La majorité des lignes de code était consacrée aux connexions avec
diverses banques de données et à des transcodages. Le cœur du programme était
une formule mathématique appliquant un résultat de la théorie des probabilités.
Une fois allégée de ses complications et réduite à son contenu logique, il
sautait aux yeux que cette formule comportait une erreur grossière. Etait-ce
erreur ou malveillance ? C’est impossible à dire. Si nous n’avions pas disposé
du code source, l’erreur n’aurait jamais pu être repérée.
Certaines études font grand usage de l’analyse des données ou de
l’économétrie. Ces méthodes comportent des pièges connus des experts mais
invisibles pour le non initié. Si par exemple l’on applique sans précautions une
régression à deux séries chronologiques, on peut faire apparaître entre elles
une forte corrélation alors qu’elles sont toutes deux corrélées avec le temps
mais nullement entre elles. (La " régression "
est la méthode statistique la plus utilisée en économétrie. Si, par hypothèse,
on suppose une variable fonction linéaire d’autres variables, la régression
permet d’estimer les coefficients de cette fonction.)
De même, si l’on applique l’analyse des correspondances à un tableau qui
n’est en aucune façons un tableau de contingence (par exemple à un tableau de
ratios), on obtiendra un résultat dépourvu de sens : son commentaire pourra
faire apparaître n’importe quelle conclusion. (Un
" tableau de contingence " est un tableau croisé représentant la ventilation
d’une population selon deux caractères qualitatifs.)
Pour un usage pertinent de la statistique
Nous n’entendons pas dénigrer la statistique, ni suggérer qu’elle serait
inutile. Cependant certains, notamment les hommes politiques, savent utiliser
les nombres avec un mélange caractéristique de maladresse et de rouerie. Le
chiffre, à la fois péremptoire et fade, usurpe la place de l’argumentation. Il
laisse sans réplique et interdit le dialogue. Alors la statistique est
prostituée, comme peuvent l’être la " bonne éducation "
qui vise à faire
" distingué ", la culture qui s’étale pour en imposer, la science
qui se dégrade en cuistrerie.
Un jour, peut-être, le conférencier qui abuse des nombres sera interpellé par
ceux qui ne le comprennent pas. Celui qui " argumente " en dévidant un chapelet
de statistiques fera rire. Celui qui veut publier un article riche en nombres et
en calculs, mais pauvre en résultats, sera recalé par le comité de lecture. Les
erreurs classiques seront visibles et donc évitées. La statistique sera alors
d’une présentation sobre, élégante et discrète. En attendant ce jour-là, la
présentation fallacieuse des nombres fera partie de la panoplie du manipulateur
qui tire parti de l’objectivité présumée du quantitatif.
|