|
Nota Bene : une première version de cette
fiche contenait une erreur de raisonnement. J'ai pu la détecter grâce à une
remarque de Jérôme Capirossi (http://www.jerome.capirossi.org/index.htm
).
Le modèle de Ricardo
permet de représenter les échanges internationaux et la spécialisation entre des
pays disposant de technologies différentes. Sous sa forme la plus simple il
comporte deux pays et deux secteurs de production. Pour construire notre modèle,
nous considérerons d’abord une économie fermée, puis une économie ouverte avec
prix exogène, et nous en déduirons les résultats d’équilibre.
Économie fermée
Considérons un pays isolé dont la population,
supposée active dans sa totalité, est d’effectif L, et dont l’économie produit
les deux biens X et Y selon des fonctions de production linéaires :
x = aLx
y = bLy
avec
Lx + Ly = L.
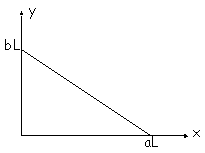
L’ensemble des productions possibles est représenté
dans le plan (x, y) par la surface d’un triangle rectangle :
Supposons que dans ce pays la fonction d’utilité du
consommateur soit une Cobb-Douglas ; en notant X = x/L et Y = y/L les
consommations par tête, on a :
U(X, Y) = cXαYβ
Nota Bene : les fonctions d’utilité étant
équivalentes à une transformation monotone croissante près, nous supposerons que
c = 1 et α + β = 1.
Pour atteindre l’optimum dans cette économie il faut
maximiser l’utilité sous la contrainte de la ressource disponible L. Cela
donne :
Lx = αL, Ly = βL
La consommation par tête est alors :
X = aα, Y = bβ,
et l’utilité est donc :
U = (aα)α(bβ)β
Économie ouverte
Supposons le pays plongé dans une économie mondiale
où se fixent les prix px et py des biens X et Y. Ces prix
sont alors pour ce pays des exogènes et la maximisation de l’utilité suppose un
choix en matière de production et de commerce extérieur :
- si py/px = a/b, les échanges extérieurs ne modifient ni
la structure de la consommation, ni le niveau de l’utilité par rapport à ce
qu’ils étaient en économie fermée.
- si par exemple py/px> a/b, le pays se spécialisera dans
la production du bien Y car cela maximise son revenu. La production par tête est
alors égale à b unités de ce bien ; l’échange par tête est tel que la valeur des
exportations soit égale à celle des importations et que l’utilité soit
maximale :
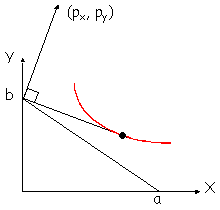
Il s'agit alors de maximiser XαYβ
sous la contrainte :
pxEx+ pyEy
= 0,
en notant Ei la quantité du produit i
échangée par tête, les importations ayant le signe plus et les exportations le
signe moins.
On trouve :
Ex
/(b
+ Ey) = αpy/βpx
d’où :
Ey = - αb et Ex = αb(py/px)
La consommation par tête est alors :
X = αb(py/px), Y = βb,
et l’utilité est :
U = b(py/px)αααββ
Équilibre général en
économie ouverte
Supposons que le monde comporte deux pays nommés 1
et 2. Nous repérerons les données propres à chaque pays (coefficients techniques
des fonctions de production, taille, consommation par tête etc.) par les indices
1 ou 2. Nous supposons que la fonction d’utilité est la même pour les deux pays.
L’économie constituée par ces deux pays est à
l’équilibre si le prix relatif py/px permet d’égaliser
les quantités échangées de part et d’autre : ce prix relatif, qui était exogène
lorsque nous considérions l’équilibre d’un pays isolé, est endogène dans
l’équilibre général d’une économie à deux pays.
Pour déterminer le prix relatif d’équilibre, il
suffit d’écrire que les quantités échangées du bien x sont égales et de signe
contraire ; l’équilibre des échanges pour le bien y en résulte.
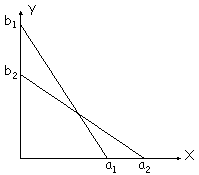
Supposons que 1 soit spécialisé dans le bien y et 2
spécialisé dans le bien x : ceci implique que l’hypoténuse du triangle rectangle
qui représente les productions possibles soit plus pentue pour 1 que pour 2,
c’est-à-dire que :
a2/b2 > py/px
> a1/b1
Les quantités échangées sont égales aux quantités
par tête multipliées par l’effectif de la population. Donc :
L1Ex1 = L1(py/px)αb1
L2Ex2 = - L2βa2
La condition de l’équilibre est :
L1Ex1 = - L2Ex2
d’où :
py/px = (β/α)(L2a2/L1b1)
Supposons que la condition suivante soit respectée :
(A) a1/b1 < (β/α)(L2a2/L1b1)
< a2/b2
Dans ce cas chaque pays est spécialisé dans la
production d'un produit. Les productions des deux pays sont :
x1 = 0, y1 = b1L1
x2 = a2L2, y2
= 0
Les consommations par tête sont :
X1 = β(L2 /L1)a2,
Y1 = βb1
X2 = αa2, Y2 = α(L1
/L2)b1
Les utilités sont :
U1 = βa2αb1β(L2 /L1)α
U2 = αa2αb1β(L1
/L2)β
Comparaison de
l’utilité des échanges
Comme (L2 /L1)a2 >
a1 et (L1 /L2)b1 > b2 les
utilités des deux pays sont plus élevées que s’ils étaient restés en autarcie.
Quel est celui des deux pays qui gagne le plus à
l’échange ? Comparons les utilités en cas d’ouverture à ce qu’elles auraient été
en cas d’autarcie :
U1/U = (βL2 a2
/αL1a1)α
U2/U = (αL1b1
/βL2b2)β
En tenant compte des inégalités (A), on vérifie que
l'échange accroît l'utilité dans chaque
pays.
Comparons les gains d'utilité :
(U1/U)/(U2/U) = L2a2αb2β
/L1a1αb1β
Le pays qui gagne proportionnellement le plus à
l’échange est celui pour lequel la quantité Laαbβ est la
plus petite. Donc si, comme nous l’avons supposé, la fonction
d’utilité des deux pays est identique (mêmes α et β), le pays qui gagne le plus
à l’échange est celui qui a les technologies les moins efficaces (plus petits a
et b) et la taille la plus petite (plus petit L).
Effet du progrès
technique
Supposons que la technologie a2
s’améliore :
a’2 = a2 + Δa2 ,
avec Δa2 > 0.
Il en résulte un accroissement proportionnel de U1
et U2 :
ΔU1/U1 =
ΔU2/U2 = αΔa2/a2
Donc un gain de l’un ou l’autre des deux pays dans
la technologie sur laquelle il s’est spécialisée entraîne pour chaque pays un
gain d’utilité égal.
Équilibre entre
« grand » et « petit » pays
Si b1L1
> b2L2 et a1L1 > a2L2,
c'est-à-dire si les quantités que 1 peut produire sont supérieures tant en ce qui concerne X
qu’en ce qui concerne Y, nous nommerons 1 "le grand pays", et 2 "le petit pays".
Nous considérons le cas où seul le petit pays est spécialisé (dans le produit Y
si b2/a2 > b1/a1), le grand pays
produisant les deux biens.
L’échange se fait alors au prix relatif interne du
grand pays :
py/px = a1/b1
L’utilité du grand pays ne s’accroît pas par
l’échange : la structure de sa consommation est en effet la même que s’il
était isolé. Par contre la structure de sa production est modifiée par l'échange, puisqu’il
peut exporter et importer pour améliorer le sort du petit pays.
Les consommations par tête du petit pays sont :
X2 = (a1/b1)αb2
Y2 = b2β
et son utilité est :
U2 = ααββ
b2(a1/b1)α
= U1(b2/b1)
Ainsi l’utilité du petit pays est :
- fonction croissante de l’efficacité a1 du grand pays dans la
production du bien dans lequel le petit pays ne s’est pas spécialisé ;
- fonction croissante de l’efficacité b2 du petit pays dans la
production du bien dans lequel il s’est spécialisé ;
-
fonction décroissante de
l’efficacité b1 du grand pays dans la production du bien dans lequel
le petit pays s’est spécialisé.
Les résultats ci-dessus deviennent évidents si
l’on considère le graphique ci-dessous. La zone de production du petit pays est représentée par le triangle rectangle, et les échanges possibles par
une demi-droite qui part du point Y = b et qui parallèle à l’hypoténuse du
triangle représentant la zone de production du grand pays.
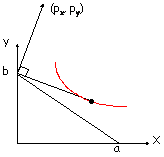
Si l’efficacité du petit pays dans la production
de Y augmente, cette demi-droite glisse vers le haut, et la courbe
d’indifférence qu'elle touche correspond à une utilité plus
élevée.
Si l’efficacité du grand pays dans la production
du bien X (non produit par le petit pays) augmente, la demi-droite pivote vers le haut et l’utilité du petit pays est
accrue.
Si l’efficacité du grand pays dans la production
du bien Y (produit par le petit pays) augmente, la demi-droite pivote vers le bas et l’utilité du petit pays est
diminuée.
Les consommations par tête du grand pays sont les
mêmes qu’en économie fermée :
X1 = a1α et Y1 = b1β,
Les consommations par tête du petit pays sont égales aux
consommations par tête du grand pays, multipliées par le coefficient b2/b1.
Ce rapport est indépendant de la valeur prise par a1.
Les productions du grand pays sont :
x1 = α(a1/b1)(b1L1+
b2L2),
y1 = βb1L1 - αb2L2
Notons que les volumes de la production du bien Y
par les pays 1 et 2 sont indépendants de la valeur de a1. Par contre,
le volume du bien X produit par le pays 1 est fonction linéaire de a1.
Calcul en valeur
Normons à 1 le prix du bien Y :
py = 1, px = b1/a1.
Le volume du bien X produit par le pays 1 croît
comme a1 et le prix est inversement proportionnel à a1 :
la valeur de la production de X sera donc la même, quel que soit a1.
La valeur des importations du bien X par le pays 2
est
Val(Ex) = αb2L2
Elle est constante quelle que soit la valeur de a1.
Les valeurs des productions sont :
Val(x2) = 0
Val(y2) = b2L2
La valeur de la production du pays 2 est donc b2L2.
Val(x1) = α(b1L1+
b2L2)
Val(y1) = βb1L1 -
ab2L2
La valeur de la production du pays 1 est donc b1L1.
Les valeurs des productions des deux pays sont
indépendantes de a1. Elles sont égales aux valeurs des consommations,
puisque les échanges sont supposés équilibrés.
Au total, une hausse de a1 a pour effet :
- une hausse proportionnelle des volumes du bien X produits, consommés,
échangés,
- une diminution proportionnelle du prix du bien X,
- aucun
changement dans les volumes du bien Y produits, consommés, échangés.
On trouvera une évolution différente si l’on utilise
un autre indice de prix. Si l’on prenait pour indice une moyenne pondérée des
prix de Y et de X, l’introduction du prix de X fera que l’indice de prix baisse,
donc que les volumes qui étaient constants dans le calcul précédent augmentent.
Les conventions retenues pour le calcul des indices suscitent donc des artefacts
qui peuvent égarer le raisonnement. Pour préciser ce point, nous avons examiné
plus en détail les questions d'indices dans la fiche suivante :
Les indices de prix et de
volume
David Ricardo, The
Principles of Political Economy and Taxation, 1817.
|