A propos des indices

Or leur calcul comporte des approximations que les utilisateurs négligent souvent, alors qu’elles délimitent la signification et la portée des indices.

Le but de la présente fiche est de revenir sur la théorie des indices afin de préciser ces limites.

La définition des indices de volume s’appuie sur la théorie économique, plus précisément sur la concavité de la fonction d’utilité du consommateur[1].

On suppose le consommateur rationnel : il répartit sa consommation entre les divers produits de façon à maximiser sa satisfaction sous la contrainte de son budget C, ce budget résultant lui-même de l’arbitrage intertemporel qui détermine la répartition du revenu entre consommation et épargne.

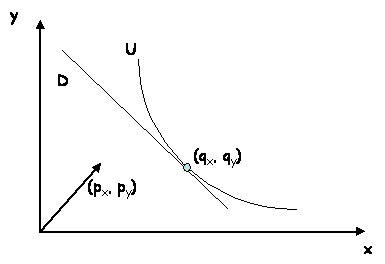
La droite budgétaire D est le lieu des points q tels que pq = C (p est le vecteur des prix des produits, q le vecteur des quantités consommées, pq est un produit scalaire). L’utilité de la consommation est U.

Considérons deux années successives et repérons la première année par l’indice 0. Lors de l'année 0, le vecteur des prix est p₀et le vecteur des quantités consommées est q₀, la droite budgétaire est D₀, l'utilité de la consommation est U₀. Lors de l'année 1, le vecteur des prix est p,le vecteur des quantités consommées est q , la droite budgétaire est D, l'utilité est U.

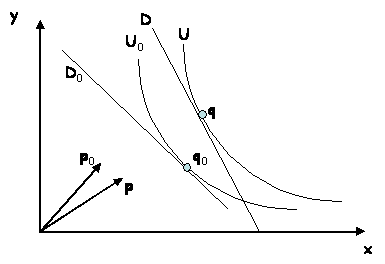
On dira que le volume de la consommation a augmenté si U > U₀. Pour mesurer cette augmentation, on considère la consommation q* qui procurerait l'utilité U si le vecteur de prix était resté identique à p₀ (le point q* est le contact entre la courbe d’indifférence U et une droite parallèle à D₀). Le budget, évalué aux prix de l’année 0, serait alors C* = p₀q*. La croissance en volume de la consommation[2] est mesurée par le rapport C*/C = p₀q* / p₀q₀.

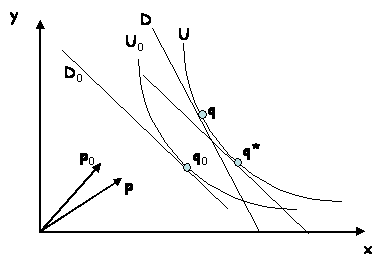
Mais comme on ne connaît pas la courbe U, il est en pratique impossible d’évaluer q*. Par défaut, on estimera p₀q* en calculant p₀q qui, lui, est observable. Selon cette convention, l’indice du volume de la consommation[3] sera p₀q / p₀q₀. Mais q* est, parmi les points de la courbe U, celui qui minimise le budget si le vecteur de prix est p₀ : donc nécessairement p₀q* ≤ p₀q. En retenant p₀q pour mesurer la croissance du volume de la consommation, on surestimera donc celle-ci.

L’indice en valeur étant pq / p₀q₀, on en déduit, pour respecter l’égalité valeur = volume*prix, l’indice de prix pq / p₀q. C’est un indice de Paasche, qui peut présenter des évolutions surprenantes car la pondération q attribuée aux divers prix varie dans le temps.

NB : on transite souvent en pratique par le calcul de l’indice de prix pour évaluer l’indice de volume, qui s’obtient alors en divisant l’indice de valeur par l’indice de prix.

La mesure de la croissance sera exacte si et seulement si p₀q* = p₀q. Le consommateur étant ici un être abstrait qui représente l'ensemble des consommateurs, on peut sans perdre en généralité supposer sa fonction d'utilité strictement concave et continûment différentiable. Alors p₀q* = p₀q implique q = q* et p = kp₀ : tous les prix devraient avoir évolué dans la même proportion et l’indice de prix serait égal à k. On peut en inférer que la surestimation de la croissance due au fait que l’on estime p₀q* par p₀q sera d’autant plus forte que les évolutions des divers prix seront plus différentes.

Considérons non plus deux, mais trois années consécutives notées 0, 1 et 2. Les indices de valeur s’enchaînent évidemment car p₂q₂ / p₀q₀= (p₂q₂ / p₁q₁)(p₁q₁ / p₀q₀). Par contre les indices de volume ne s’enchaînent pas : p₀q₂ / p₀q₀n’est pas égal à
(p₁q₂ / p₁q₁)(p₀q₁ / p₀q₀). Les indices de prix, eux non plus, ne s’enchaînent pas.

Dans la pratique du calcul on multiplie souvent entre eux les indices successifs comme s’ils s’enchaînaient. Le résultat ainsi obtenu n’est pas exact et le sera d’autant moins que le calcul porte sur un plus grand nombre d’années.

Pour corriger ce défaut on calcule parfois des indices « au prix d’une année de base ». Prenons pour année de base l’année 0. Les indices de volume des deux années suivantes seront p₀q₁ / p₀q₀et p₀q₂ / p₀q₀, la croissance du volume entre les années 1 et 2 étant alors estimée par l’indice p₀q₂ / p₀q₁. Cette méthode, appliquée plusieurs années de suite, fournit des indices qui s’enchaînent. Mais comme avec le temps les proportions entre les prix p s’écartent de plus en plus de la structure de base p₀, la surestimation de la croissance commise en estimant p₀q* par p₀q ira s’aggravant et il faudra, après quelques années, changer d’année de base.

1) L'hypothèse de la rationalité des agents économiques, qui se trouve au point de départ de la théorie des indices, est commode au plan théorique mais contredite par l'expérience (cf. les travaux d'Herbert Simon, et plus récemment Choices, Values and Frames de Daniel Kahneman et Amos Tversky, Cambridge University Press 2000). La mesure du volume de la production en sera altérée lorsque l'incertitude est élevée ou lorsque l'innovation est forte, circonstances qui accroissent le risque de non-rationalité.

2) Quelle que soit la méthode retenue (indice chaîne ou année de base), l’évaluation de la croissance en volume par un indice ne fournit un résultat interprétable que sur un intervalle de quelques années successives. Le calcul qui enchaînerait des indices sur des dizaines d’années fournit certes un résultat numérique, mais la signification de celui-ci sera douteuse.

3) Si les prix des divers produits croissent tous à la même vitesse, le calcul des indices est exact et les problèmes que pose leur enchaînement disparaissent. L’utilisation courante des indices et de leur enchaînement postule, de façon implicite, que tous les prix évoluent parallèlement. Cette hypothèse fait violence à l’observation.

4) La théorie des indices est bâtie sur la fonction d’utilité du consommateur. Cependant une fois le formalisme du calcul élaboré autour de quantités de type p₀q, on l’applique au PIB, à l’investissement, au commerce extérieur, tous agrégats qui n’ont pas avec la fonction d’utilité un rapport aussi étroit que la consommation. Le calcul fournit ainsi des indicateurs de prix et de volume dont la signification économique n’est pas claire.

5) La fonction d’utilité sur laquelle s’appuie la théorie des indices est définie, de façon classique, comme une fonction ordinale croissante du volume de la consommation de certains produits ou agrégats de produits. Cette définition impose des limites à la signification économique des indices :

a. Si un produit nouveau surgit lors de l’année 1 pour prendre sa place dans la fonction d’utilité (que l’on pense au téléphone mobile, au baladeur, au lecteur de DVD etc.), on ne dispose pas d’une observation de son prix ni de son volume lors de l’année 0. On ne peut donc pas tenir compte de cette nouveauté dans le calcul de l’indice, et il ne pourra y figurer que lors de l’année 2. Si le produit appartient à un agrégat plus vaste cette difficulté semble disparaître, mais elle est en fait reportée sur l’évaluation du volume et du prix de cet agrégat.

b. Dans les faits l’utilité ne dépend pas du seul volume mais aussi de la qualité de chaque produit. On s’est efforcé de prendre en compte la qualité des produits en calculant des indices hédoniques ; comme il est cependant difficile d’évaluer le gain en volume qui serait, du point de vue de l’utilité, l’équivalent d’un gain en qualité, l'interprétation des indices hédoniques est des plus délicates. L'effet qualité est vraisemblablement sous-estimé.

6) En pratique, le calcul des indices suppose de nombreuses conventions : choix des agrégats sur lesquels porte l’observation ; indice chaîne ou recours à l’année de base ; traitement de l’effet qualité etc. La comparaison des indices (et des taux de croissance) entre périodes différentes ou pays différents nécessite des corrections qu’il est parfois impossible d’effectuer.

7) La fragilité des indices et la difficulté des comparaisons se répercutent sur les indicateurs construits en s’appuyant sur eux, notamment sur les indicateurs de productivité obtenus en divisant le volume produit par la quantité de travail.

8) Le réalisme du raisonnement économique s’obtient non en s’appuyant sur des indices (ou, ce qui revient au même, sur des indicateurs de volume et de prix), mais en posant des hypothèses simples et en étalonnant les paramètres sur des ordres de grandeur observés et bien choisis. Cela n’enlève pas tout intérêt aux indices, car ils fournissent des ordres de grandeur, mais ils ne peuvent à eux seuls ni alimenter un raisonnement, ni fonder une démonstration.

9) Étalonner une équation économétrique sur des indicateurs de volume et de prix, comme on le fait souvent, c’est prendre le risque de reporter sur les coefficients de l’équation les biais et écarts de principe dont souffre le calcul des indices.

[1] Une bonne part du raisonnement macroéconomique relève de la robinsonnade : on y traite un pays entier comme s’il s’agissait d’un seul individu muni d’une fonction de production et d’une fonction d’utilité, la spécification de ces fonctions et les ordres de grandeur étant induits de l’observation de l’économie réelle (modèle de croissance de Ramsey, modèle des échanges internationaux de Heckscher-Ohlin etc.). Le raisonnement ne considère les personnes et les institutions (État, entreprises) que quand il porte sur ce qui se passe à l'intérieur de l'"individu" agrégé qu'est un pays : répartition du patrimoine, distribution et redistribution des revenus, échanges entre branches du système productif etc.

[2] On ne mesure donc pas la croissance de l’utilité – cela n’aurait pas de sens, l’utilité étant une fonction ordinale de la consommation – mais la croissance du budget consacré à la consommation, évalué à prix constants.

[3] On suppose ici que l’indice est de la forme 1 + τ, où τ est un taux de croissance.