|
Sortir de l'embarras
15 juin 2002
- (cf. "Complexité
et complication")
-
- Page précédente : Les
embarras de la complication
Nous ferons un grand progrès
dans notre démarche intellectuelle et dans nos entreprises lorsque nous aurons
pris l’habitude de rire de celui qui dit « ce n’est pas si simple !
», « il faut bien répondre à la demande des utilisateurs » ou
tout autre phrase qui révèle un refus de la simplicité de la pensée. Il faut
se servir des mécanismes de la mode, fussent-ils cruels, pour extirper les
mauvaises habitudes. La seule question qui convienne lorsque quelqu'un présente
un modèle est : « est-ce la bonne simplification ? »
Un modèle doit être à la
fois sobre (principe d’économie) et pertinent (principe d’efficacité). La
justesse de ces principes résulte de la complexité inhérente au réel et de
notre incapacité à le penser entièrement. Il faut percevoir cette incapacité
non comme un manque, un défaut, mais comme une force : elle est condition nécessaire
de l'action et de la formation du « coup d’œil », de même
que l'imperfection de notre mémoire est condition nécessaire de notre capacité
à créer des concepts (cf. Les
embarras de la complication).
Pour sortir de l'embarras, il
faut assumer et cultiver la simplicité de la pensée. On peut aussi s'appuyer
sur quelques outils méthodologiques : modèle en couches ; croisement des découpages
; raisonnement probabiliste ; élaboration de la pertinence par des
consultations et validations, etc.
On rencontre en informatique
des difficultés d'origine technique : par abus de langage, on les baptise du
terme « complexité ». Elles ne relèvent pas exactement de la présente étude,
mais il est intéressant de les examiner (cf. "Complexité" en informatique).
Le modèle en couches
Un modèle en couches consiste
en l'articulation de plusieurs sous-modèles, nommés « couches » [Tanenbaum].
Celles-ci sont caractérisées chacune par un protocole spécifique et
reliées entre elles par des interfaces. On utilise le modèle en couches
pour représenter des situations où plusieurs logiques jouent simultanément.
Certes, le nombre des logiques ainsi articulées reste fini et on n'atteint donc
pas la richesse de la complexité ; mais le modèle en couches, tout en restant
pensable pour un être humain, possède l'un des traits de la complexité : la
pluralité des logiques.
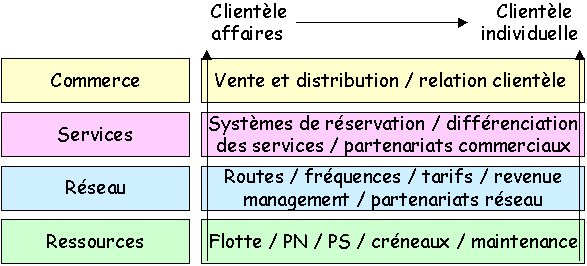
Son
domaine d’application est très vaste. Nous l'avons utilisé pour décrire l'économie du transport
aérien, en représentant l'activité d'un transporteur selon plusieurs couches
(cf. chapitre "transport aérien"
de "e-conomie") :
Nous l'avons utilisé aussi
pour modéliser les systèmes d'information,
le fonctionnement de l'ordinateur, l'apport
des NTIC à l'économie, etc. On trouvera une présentation technique du
modèle en couches dans le chapitre "modèle
en couches" de "e-conomie",
et une présentation philosophique dans "A propos du modèle en couches".
Croiser
les découpages
Lorsque
l'on considère une même population selon diverses grilles, on opère sur cette
population plusieurs partitions (exemple : considérer une population d'êtres
humains selon la tranche d'âge et selon la région de résidence). « Croiser
les découpages », c'est considérer le produit de deux partitions (le
tableau qui donne la ventilation de la population, et où chaque ligne représente
une région, chaque colonne une tranche d'âge). Un tel tableau est nommé
« tableau de contingence », ou encore « tableau croisé ».
Son étude permet d'examiner la corrélation entre les deux grilles ; l'expérience
montre qu’elle est riche en enseignements. Il est donc utile, lorsque l'on
examine une même réalité selon deux grilles conceptuelles, d'établir le
tableau croisé et de l’examiner. Les statisticiens utilisent à cette fin
l'analyse factorielle des correspondances. Pour une étude rapide, un calcul
simple peut suffire [Volle 3].
Imprévisibilité et probabilité
Les sciences physiques du début
du XIXème siècle postulaient le déterminisme : l'évolution d'un système était
déterminée une fois connues les positions et vitesses initiales ; on en déduisait
que l'avenir était prévisible.
Les sciences physiques étant
alors le modèle de toute science, le déterminisme a étendu son empire sur
tous les domaines de la connaissance, même sur ceux comme l'histoire, l'économie,
la sociologie où sa pertinence est douteuse. Le choc n'en a été que plus
profond lorsque la physique elle-même a imposé des limites au déterminisme :
à l'échelle subatomique, il est d'après le principe d'incertitude de
Heisenberg impossible de mesurer simultanément et de façon précise la
position et la vitesse d'une particule : le mouvement d'une particule est
probabiliste.
A vrai dire on aurait pu
constater qu'à l'échelle macroscopique la prévisibilité est contredite par
l'expérience : si les physiciens pouvaient prédire le résultat d'un coup de dés,
cela se saurait dans les salles de jeu. Certes ce résultat est déterminé par
les conditions du lancer, mais comme la consistance souple de la main du lanceur
interdit de les connaître avec précision, en pratique le résultat d'un
lancer est probabiliste tout comme la loi du mouvement d'une particule.
L'imprévisibilité existe
aussi dans les systèmes planétaires. Les phénomènes régis par des équations
différentielles non linéaires, bien que déterministes par nature, donnent
naissance à des effets chaotiques qui ne peuvent pas être distingués d'un
comportement probabiliste. En outre ils sont, comme le lancement d'un dé, très
sensibles aux conditions initiales [Gleick
1]. Ainsi on ne peut pas garantir que la terre ne quittera jamais le système
solaire : la prévision de sa trajectoire, probabiliste, est entourée d'un halo
d'incertitude qui s'élargit à mesure que l'on s'éloigne dans le futur.
La science économique a créé
une branche spéciale pour traiter l'incertitude : c'est la théorie du risque
à laquelle elle associe la théorie des anticipations. Un entrepreneur doit
savoir raisonner en avenir incertain. Il en est de même du stratège qui doit
prendre des décisions justes alors qu'il reçoit des rapports partiels, parfois
erronés, et que l'ennemi fait tout pour l'induire en erreur. Il existe des généraux
qui gagnent les batailles et des dirigeants efficaces : ce sont ceux qui possèdent
le « coup d'œil », faculté qui permet de traiter au mieux les
situations incertaines.
Cette faculté s'acquiert par l'exercice. Ceux qui la possèdent sont efficaces
dans l'action mais ils n'ont généralement ni le goût, ni la capacité
d'expliquer leurs raisonnements [Clausewitz].
Ainsi dans beaucoup de domaines
il faut savoir raisonner sur des probabilités, gérer des incertitudes, assumer
des risques. Si l'on explicite le raisonnement, on verra qu'il fait appel au
calcul des probabilités. Certaines personnes ont le talent de raisonner juste
dans un contexte incertain sans pourtant rien connaître au calcul des
probabilités. Chez d'autres, au contraire, la faculté de raisonner semble
paralysée dès que se présente une incertitude.
Limites de la logique
Au début du XXème siècle,
plusieurs logiciens dont Bertrand Russell est le plus connu se sont efforcés de
donner aux mathématiques un fondement à la fois logiquement correct (non
contradiction) et complet (pouvoir démontrer toute proposition vraie). Kurt Gödel
a démontré en 1931 que quel que soit le système d'axiomes utilisé pour
fonder une théorie, il existe des propositions que l'on sait vraies mais dont
la vérité ne peut pas être démontrée dans le cadre du système [Gödel].
Donc quelle que soit la richesse d'un système d'axiomes elle ne peut égaler la
complexité du contenu potentiel de la pensée (cf. petit résumé du
théorème de Gödel).
La pensée apparaît ainsi
comme complexe, puisque aucune théorie ne peut en rendre compte. Or nous avons
dit que la pensée était simple. Il n'y a pas cependant ici de contradiction :
la pensée complexe, c'est la pensée potentielle, constituée par
l'ensemble des propositions que l’on peut déduire de l’ensemble des
batteries d’axiomes possibles ; mais la pensée explicite, résultat de nos réflexions,
est fondée sur un nombre fini d'axiomes. Le théorème de Gödel montre que la
pensée explicite est plus simple que la pensée potentielle.
La logique ne peut donc pas
avoir réponse à tout. Nous nous en doutions un peu, mais certains logiciens
s'opposaient à cette intuition avec une certaine raideur. Grâce à Gödel la
logique elle-même a apporté, de l'intérieur de ses propres méthodes, la
preuve qu'elle avait des limites : dans tout système, il existe des vérités
indémontrables.
La logique est condition nécessaire
de l'efficacité pratique de la pensée, car une pensée incohérente est
pratiquement nulle ; par contre, la logique n'est pas condition suffisante de la
pertinence de la pensée, de l'adéquation de la pensée à une situation (cf. Simplicité de la
pensée). Le caractère logique d'un système ne prouve pas sa pertinence
face à une situation particulière : un délire peut être cohérent.
Écoute
Comment peut-on élaborer la
pertinence, l'adéquation à l'action ? Pour comprendre une situation particulière,
faire le choix des concepts qui permettent d'en rendre compte, élaborer une théorie
pertinente, la pensée pure ne suffit pas : il faut en outre la démarche
expérimentale. Lorsque l'on veut construire un système d'information, il
faut utiliser l'expérience des utilisateurs, tenir compte des intentions des
stratèges. L'écoute est non seulement une attitude respectueuse envers l'autre
et donc convenable au plan moral, c'est une étape méthodologique nécessaire.
Durant la phase d'écoute, la
grille conceptuelle de l'auditeur est mise entre parenthèses (si ce n'est la
grille propre à l'écoute elle-même) ; il accepte d'entrer dans des
constructions intellectuelles qui ne lui sont pas familières, de faire le
voyage mental que cela implique. Il y faut un effort de modestie parfois pénible
: celui qui entre dans un domaine nouveau pour lui joue le rôle du bizut et se
fait souvent maltraiter par les experts. Quand le bizut prend ses repères, se
familiarise et commence à parler avec quelque autorité, les experts n'apprécient
guère de le voir ainsi contourner les complications qui protégent leur spécialité.
Le climat se gâte, c'est un moment délicat.
Le pire ennemi de l'auditeur,
c'est la "tache aveugle" de
l'intellect ([Volle 2], p. 234), la tentation de
ne pas tenir compte de choses que l'on entend, mais que l'on juge négligeables
parce qu'elles sont contrariantes. Ceux qui ont un tempérament impérieux, les enfants gâtés,
sont incapables d'écouter ; il leur est donc difficile d’accéder à la
pertinence même s’ils sont intellectuellement brillants. C'est pourquoi des
personnes douées des plus grands talents intellectuels sont parfois, de façon
surprenante, inaptes à l'action.
Après l'écoute doit venir la
synthèse. Il ne faut pas croire tout ce que l'on entend dire ; les habitudes
des praticiens du terrain sont parfois illogiques, car elles découlent de méthodes
anciennes qui se sont superposées et que les corporations ont dogmatisées. En élucidant les
processus, l'auditeur apporte une valeur ajoutée : il rend les incohérences
visibles et permet au besoin de mise en ordre de s'exprimer. Nous avons décrit
ailleurs les méthodes nécessaires pour remonter de la demande aux
besoins et pour obtenir une validation authentique.
|